Wyjaśnialność modeli - metryki statystyczne - tutorial#
Wstęp#
O modelach uczenia maszynowego w ogólnym pojęciu możemy mówić jako o czarnych skrzynkach (eng. “black box”). Wiemy, że podając do wytrenowanego modelu pewne określone wcześniej argumenty otrzymamy pewną predykcję oczekiwanej wartości. Ostatecznie mamy nadzieję, że wyniki podane przez model będą, jak najbliżej wartości, które byśmy zaobserwowali w rzeczywistości przy określonych parametrach (argumenty modelu).
Pojawiają się tutaj dwa miejsca, które są w stanie dostarczyć nam wiedzy na temat jakości naszego modelu. Na jakość modelu składa się zarówno sposób w jaki model dochodzi do tego wyniku, sposób jego działania, jak i wynik predykcji modelu.
Część dotycząca tego w jaki sposób model podejmuje końcową decyzje, skupia się na wyjaśnieniu tego, jak poszczególne argumenty dostarczone do modelu są przez niego interpretowane i jak wpływają na końcowy wynik predykcji. Proces ten nazywamy XAI (“Explainable AI”), czyli wyjaśnialność modelu. O tym w jaki sposób możemy podejść do wyjaśnienia tego co siedzi wewnątrz modelu dowiemy się w kolejnym module.
W tym module skupimy się na tej drugiej części, która pozwoli poznać jakość naszego modelu, a mianowicie na interpretacji wyników predykcji. Projektując modele uczenia maszynowego dążymy, aby model odznaczał się jak najlepszym odwzorowaniem wartości rzeczywistych za pomocą predykcji przy zadanych parametrach. W tym celu wyliczamy pewne miary, nazywane metrykami, które pozwalają ocenić grupowo wyniki predykcji względem wartości rzeczywistych.
Nie wszystkie problemy biznesowe, na których potrzeby chcemy odpowiedzieć, będziemy w stanie dobrze ocenić tymi samymi metrykami. Oraz nie każda z metryk będzie potrafiła odpowiedzieć nam na wszystkie wątpliwości na temat jakości naszej predykcji. Stąd bardzo ważnym krokiem jest odpowiedni dobór metryki dopasowanej pod problem biznesowy, który staramy się rozwiązać. Na podstawie wyników z tej metryki, bądź kilku metryk, będziemy podejmować dalsze decyzje o rozwoju modelu. Tak, więc wybór nieodpowiedniej metryki może spowodować wyciągnięcie błędnych wniosków oraz błędne określenie dalszych kroków prac nad modelem.
Omawiane błędy dla danych typów predykcji#
Modele Regresyjne |
Modele Klasyfikacyjne |
Modele Grupujące |
|---|---|---|
ME |
Macierz pomyłek |
V-measure |
MAE |
Accuracy |
Silhouette Coefficient |
MSE |
Precision |
Davies-Bouldin Index |
RMSE |
F-score |
Dunn’s Index |
MSLE |
ROC |
|
MAPE |
AUC |
|
SMAPE |
Zaprezentowane metryki zostały pokrótce omówione w części wykładowej.
W tym tutorialu skupimy się głównie na wyliczaniu metryk dla podanych przykładów oraz na interpretacji ich wartości.
Większość metryk została zaimplementowana i jest dostępna poprzez bibliotekę scikit-learn.
Jeśli chcemy znaleźć metrykę dla naszego modelu, a żadna z nam znanych nie spełnia założonych kryteriów warto tutaj zajrzeć:
https://scikit-learn.org/stable/modules/model_evaluation.html
Podejście Regresyjne#
Podstawowym podejściem na którym wyliczamy większość z błędów w regresji jest różnica pomiędzy wartością oczekiwaną, a predykcją otrzymaną z modelu. Różnicę tą nazywamy błędem predykcji - z ang. Error
Jako \(y_i\) będziemy oznaczać pojedyńczą rzeczywistą obserwacje ze zbioru \(N\) elementów, natomiast \(\hat{y_i}\) będzie reprezentować predykcje odpowiadającą tej obserwacji. Wartość \(\overline{y}\) oznaczać będzie natomiast średnią ze wszystkich obserwacji.
ME#
W celu obliczenia średniego błędu na całym zadanym zbiorze używamy najbardziej podstawowej metryki, czyli średniego błędu - z ang. Mean Error
Interpretujemy ją jako średnią odległość pomiędzy wartościami rzeczywistymi, a predykcjami naszego modelu.
Metryka ta posiada jedną dość istotną wadę. Dla błędów o takiej samej sile, lecz przeciwnym kierunku następuje redukcja wpływu tych błędów na końcową wartość metryki, co ukrywa niedoskonałości modelu.
import numpy as np
import matplotlib.pyplot as plt
def mean_error(y, y_hat):
"""
Funkcja pozwalająca na wyliczenie wartości Mean Error
:param y: wektor wartości rzeczywistych
:param y_hat: wektor wartości przewidywanych
:return: średni błąd na obserwacjach
"""
# y oraz y_hat są reprezentowane poprzez wektory
# jeśli wykonamy obliczenie różnicy między nimi to powstanie rónież wektor
# wyliczenie średniej z biblioteki numpy spowoduje wyliczenie średniej z wartości takiego wektora
return np.mean(y-y_hat)
x = np.array([1,2,3,4]) # argumenty
y = np.array([0,5,6,3]) # wartości
plt.plot(x,y,'o') # wizualizacja wartości rzeczywistych
m,b = np.polyfit(x,y,1) # regresja liniowa (model)
plt.plot(x, m*x+b) # wizualizacja predykcji modelu (żółta)
y_hat_linear = m*x+b # predykcje modelu liniowego
a1,a2,c = np.polyfit(x,y,2) # regresja wielomianem drugiego stopnia (model)
plt.plot(x, a1*np.power(x,2) + a2*x + c) # wizualizacja predykcji (zielona linia)
y_hat_poly = a1*np.power(x,2) + a2*x + c # predykcje modelu wielomianowego
plt.legend(['y', 'liniowa', 'wielomianowa']) # dodanie legendy
plt.show() # wizualizacja
print(f"Błąd Mean Error dla regresji liniowej: {np.round(mean_error(y, y_hat_linear),1)}")
print(f"Błąd Mean Error dla regresji wielomianowej: {np.round(mean_error(y, y_hat_poly),1)}")
Błąd Mean Error dla regresji liniowej: 0.0
Błąd Mean Error dla regresji wielomianowej: -0.0
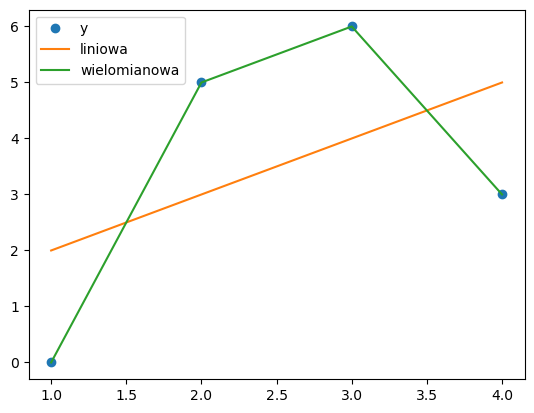
Jak możemy zaobserwować, zarówno dla regresji liniowej, jak i wielomianowej średni błąd dla modelu wyniósł zero.
Bazując tylko na tej metryce moglibyśmy powiedzieć, że oba z modeli osiągają jednakowy wynik. Dopiero wizualizacja pozwala nam zaobserwować, że tak naprawdę regresja liniowa jest mocnym przybliżeniem tego co byśmy oczekiwali.
MAE#
W celu uniknięcia złych interpretacji częściej używa się metryki średniego błędu bezwzględnego - z ang. Mean Absolute Error
\(MAE=\frac{1}{N} \sum^N_{i=1} | y_i-\hat{y_i} |\)
def mean_absolute_error(y, y_hat):
"""
Funkcja pozwalająca na wyliczenie wartości Mean Absolute Error
:param y: wektor wartości rzeczywistych
:param y_hat: wektor wartości przewidywanych
:return: średni błąd bezwzględny na obserwacjach
"""
return np.mean(np.abs(y-y_hat))
print(f"Błąd Mean Absolute Error dla regresji liniowej: {np.round(mean_absolute_error(y, y_hat_linear),1)}")
print(f"Błąd Mean Absolute Error dla regresji wielomianowej: {np.round(mean_absolute_error(y, y_hat_poly),1)}")
Błąd Mean Absolute Error dla regresji liniowej: 2.0
Błąd Mean Absolute Error dla regresji wielomianowej: 0.0
Po zastoswaniu błędu MAE widzimy, że model używający regresji liniowej dla naszego przypadku myli się średnio o 2 jednostki względem wartości rzeczywistych. Jest to poprawne wyjaśnienie jakości dla zaprezentowanego, prostego przypadku.
Zestawiając obok siebie błąd MAE oraz ME pozwala zyskać natomiast dodatkową informacje.
O ile błąd MAE trafniej pozwoli określić nam o ile się średnio mylimy podczas predykcji to zestawiając wraz z błędem ME możemy otrzymać informację w którą stronę częściej się mylimy. Czy nasze predykcje względem wartości rzeczywistych są częściej zawyżane, czy zaniżane.
x = np.array([1,2,3,4,5,6]) # argumenty
y = np.array([1,3,2,3,2,4]) # wartości
plt.plot(x,y,'o') # wizualizacja wartości rzeczywistych
m,b = np.polyfit(x,y,1) # regresja liniowa (model)
plt.plot(x, m*x+b) # wizualizacja predykcji modelu (żółta)
y_hat_linear = m*x+b # predykcje modelu liniowego
b2 = b+2
plt.plot(x, m*x+b2) # wizualizacja predykcji modelu (zielona)
y_hat_linear_up = m*x+b2 # predykcje modelu liniowego zawyżonego
b3 = b-1
plt.plot(x, m*x+b3) # wizualizacja predykcji modelu (czerwona)
y_hat_linear_down = m*x+b3 # predykcje modelu liniowego zaniżonego
plt.legend(['y', 'liniowa', 'liniowa_up', 'liniowa_down']) # dodanie legendy
plt.show() # wizualizacja
print(f"Błąd Mean Error dla regresji liniowej: {np.round(mean_error(y, y_hat_linear),1)}")
print(f"Błąd Mean Error dla regresji liniowej zawyżonej: {np.round(mean_error(y, y_hat_linear_up),1)}")
print(f"Błąd Mean Error dla regresji liniowej zaniżonej: {np.round(mean_error(y, y_hat_linear_down),1)} \n")
print(f"Błąd Mean Absolute Error dla regresji liniowej: {np.round(mean_absolute_error(y, y_hat_linear),1)}")
print(f"Błąd Mean Absolute Error dla regresji liniowej zawyżonej: {np.round(mean_absolute_error(y, y_hat_linear_up),1)}")
print(f"Błąd Mean Absolute Error dla regresji liniowej zaniżonej: {np.round(mean_absolute_error(y, y_hat_linear_down),1)}")
Błąd Mean Error dla regresji liniowej: 0.0
Błąd Mean Error dla regresji liniowej zawyżonej: -2.0
Błąd Mean Error dla regresji liniowej zaniżonej: 1.0
Błąd Mean Absolute Error dla regresji liniowej: 0.6
Błąd Mean Absolute Error dla regresji liniowej zawyżonej: 2.0
Błąd Mean Absolute Error dla regresji liniowej zaniżonej: 1.0
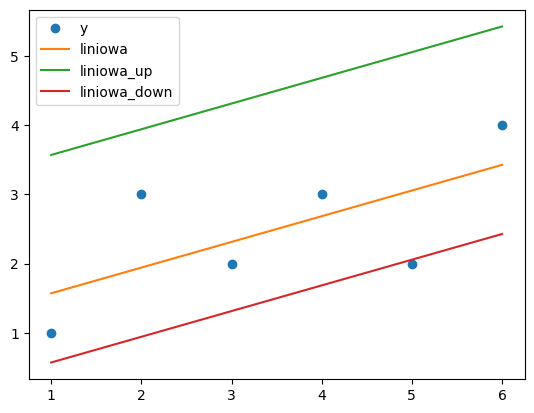
Interpretując powyższe wyniki jesteśmy w stanie zauważyć, że model liniowy zawyżony faktycznie zawyża wyniki na co wskazuje znak ‘-’ przy metryce ME. Oznacza to, że średnio większość obserwacji rzeczywistych była niższa, niż wartość predykcji z modelu.
Odwrotnie natomiast jest w przypadku modelu zaniżonego, gdzie widzimy, że błąd ME osiągnął wartość dodatnią.
MSE#
Kolejną ważną metryką jest metryka związana z kwadratem błędu, czyli średni kwadrat błędu - z ang. Mean Square Error
Reprezentuje ta wartość wariancję wśród odległości pomiędzy wartościami rzeczywistymi, a predykcją.
\(MSE=\frac{1}{N} \sum^N_{i=1}(y_i-\hat{y_i})^2\)
Dużym minusem tej metryki jest interpretowalność. Ze względu na to, że obliczana jest ona na podstawie kwadratu odległości pomiędzy wartościami, jednostka w jakiej jest reprezentowana jest również kwadratem jednostki, w której reprezentujemy predykcję.
Plusem, który stoi za popularnością tej metryki jest jej różniczkowalność, co pozwala na wykonywanie na tej metryce różnych operacji matematycznych w przeciwieństwie do MAE, które jest nieróżniczkowalne. Konsekwencją tego jest użycie wartości MSE w wyliczaniu innych metryk, jak na przykład RMSE.
Dodatkową charakterystyczną rzeczą dla metryki MSE jest jej wrażliwość na wartości odstające. Może to być traktowane jako wada, jak i zaleta. Z jednej strony posiadając bardzo dobrze dopasowany model z pojedyńczym, lecz wysokim odchyleniem od wartości rzeczywistej uzyskujemy podobny błąd co do modelu, który jest dość przeciętny, jednak wartości predykcji znajdują się w węższym zakresie wartości.
Jednakże, chcąc stworzyć dobry model oczekujemy od niego, że będzie on w miarę stabilny i mniej wrażliwy na odchylenia wśród wartości. Z uwagi na to metryka ta jest dobrą metryką do monitorowania naszego modelu pod kątem stabilności predykcji.
def mean_square_error(y, y_hat):
"""
Funkcja pozwalająca na wyliczenie wartości Mean Square Error
:param y: wektor wartości rzeczywistych
:param y_hat: wektor wartości przewidywanych
:return: średni kwadrat błędu na obserwacjach
"""
return np.mean(np.power(y-y_hat,2))
x = np.array([1,2,3,4,5,6]) # argumenty
y = np.array([1,2,1,1,1,1]) # wartości
y_2 = np.array([1,1.5,1.5,1,1,1])
y_3 = np.array([1,3,1,1,1,1])
plt.plot(x,y,'o') # wizualizacja wartości rzeczywistych
plt.plot(x,y_2) # wizualizacja wartości rzeczywistych
plt.plot(x,y_3) # wizualizacja wartości rzeczywistych
plt.legend(['y', 'model_1', 'model_2']) # dodanie legendy
plt.show() # wizualizacja
print(f"Błąd Mean Absolute Error dla model_1: {np.round(mean_absolute_error(y, y_2),1)}")
print(f"Błąd Mean Absolute Error dla model_2: {np.round(mean_absolute_error(y, y_3),1)}\n")
print(f"Błąd Mean Square Error dla model_1: {np.round(mean_square_error(y, y_2),1)}")
print(f"Błąd Mean Square Error dla model_2: {np.round(mean_square_error(y, y_3),1)}")
Błąd Mean Absolute Error dla model_1: 0.2
Błąd Mean Absolute Error dla model_2: 0.2
Błąd Mean Square Error dla model_1: 0.1
Błąd Mean Square Error dla model_2: 0.2
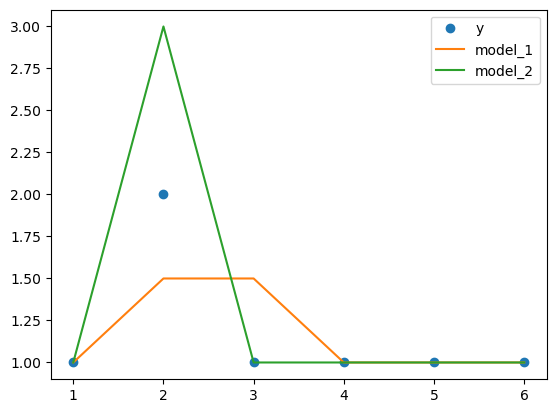
W powyższym przykładzie możemy zobserwować, że dla modelu drugiego, który bardzo wrażliwie zareagował na zmianę, metryka MSE pokazała wyższy błąd, niż dla modelu pierwszego. Mimo, że błędy MAE dla obu modeli są jednakowe, po dodaniu błędu MSE zyskaliśmy świadomość, który z tych dwóch modeli będzie bardziej zachowawczy w przyszłych predykcjach.
RMSE#
Pewną korektą dla błędu MSE jest błąd RMSE, który posiada ułatwioną interpretację ze względu na taką samą jednostkę, jak dla wartości, które predykujemy. Błąd RMSE jest to pierwiastek kwadratowy z błędu MSE - z ang. Root Mean Square Error
\(RMSE=\sqrt{\frac{1}{N} \sum^N_{i=1}(y_i-\hat{y_i})^2}\)
def root_mean_square_error(y, y_hat):
"""
Funkcja pozwalająca na wyliczenie wartości Root Mean Square Error
:param y: wektor wartości rzeczywistych
:param y_hat: wektor wartości przewidywanych
:return: pierwiastek średniego kwadratu błędu na obserwacjach
"""
return np.sqrt(np.mean(np.power(y-y_hat,2)))
x = np.array([1,2,3,4,5,6]) # argumenty
y = np.array([1,2,1,1,1,1]) # wartości
y_2 = np.array([1,1.5,1.5,1,1,1])
y_3 = np.array([1,3,1,1,1,1])
plt.plot(x,y,'o') # wizualizacja wartości rzeczywistych
plt.plot(x,y_2) # wizualizacja wartości rzeczywistych
plt.plot(x,y_3) # wizualizacja wartości rzeczywistych
plt.legend(['y', 'model_1', 'model_2']) # dodanie legendy
plt.show() # wizualizacja
print(f"Błąd Mean Absolute Error dla model_1: {np.round(mean_absolute_error(y, y_2),1)}")
print(f"Błąd Mean Absolute Error dla model_2: {np.round(mean_absolute_error(y, y_3),1)}\n")
print(f"Błąd Mean Square Error dla model_1: {np.round(mean_square_error(y, y_2),1)}")
print(f"Błąd Mean Square Error dla model_2: {np.round(mean_square_error(y, y_3),1)}\n")
print(f"Błąd Root Mean Square Error dla model_1: {np.round(root_mean_square_error(y, y_2),1)}")
print(f"Błąd Root Mean Square Error dla model_2: {np.round(root_mean_square_error(y, y_3),1)}")

Błąd Mean Absolute Error dla model_1: 0.2
Błąd Mean Absolute Error dla model_2: 0.2
Błąd Mean Square Error dla model_1: 0.1
Błąd Mean Square Error dla model_2: 0.2
Błąd Root Mean Square Error dla model_1: 0.3
Błąd Root Mean Square Error dla model_2: 0.4
RMSLE#
W przypadku biznesu, jak na przykład LPP, znaczące jest to w którą stronę się myli. To znaczy, czy nasze błędy są przeszacowane, bądź niedoszacowane. Stosując miary oparte o kwadrat odległosci pomiędzy wartościami rzeczywistymi, a przewidywanymi gubimy tą informacje. W takim celu możemy użyć metryki, która jest odpowiednikiem dla RMSE (oraz MSE), a mianowicie RMSLE (MSLE) - z ang. Root Mean Square Logarithmic Error
\(RMSLE=\sqrt{\frac{1}{N} \sum^N_{i=1}(log_e(1+y_i)-log_e(1+\hat{y_i}))^2}\)
def root_mean_square_logarithmic_error(y, y_hat):
"""
Funkcja pozwalająca na wyliczenie wartości Root Mean Square Logarithmic Error
:param y: wektor wartości rzeczywistych
:param y_hat: wektor wartości przewidywanych
:return: pierwiastek średniego kwadratu błędu zlogarytmowawanego na obserwacjach
"""
return np.sqrt(np.mean(np.power(np.log(1+y)-np.log(1+y_hat),2)))
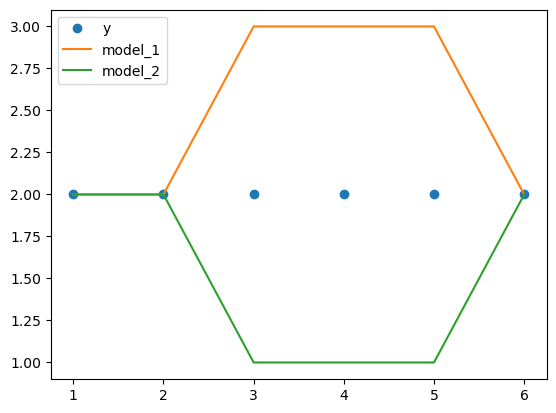
x = np.array([1,2,3,4,5,6]) # argumenty
y = np.array([2,2,2,2,2,2]) # wartości
y_2 = np.array([2,2,3,3,3,2])
y_3 = np.array([2,2,1,1,1,2])
plt.plot(x,y,'o') # wizualizacja wartości rzeczywistych
plt.plot(x,y_2) # wizualizacja wartości rzeczywistych
plt.plot(x,y_3) # wizualizacja wartości rzeczywistych
plt.legend(['y', 'model_1', 'model_2']) # dodanie legendy
plt.show() # wizualizacja
print(f"Błąd Mean Absolute Error dla model_1: {np.round(mean_absolute_error(y, y_2),1)}")
print(f"Błąd Mean Absolute Error dla model_2: {np.round(mean_absolute_error(y, y_3),1)}\n")
print(f"Błąd Root Mean Square Error dla model_1: {np.round(root_mean_square_error(y, y_2),1)}")
print(f"Błąd Root Mean Square Error dla model_2: {np.round(root_mean_square_error(y, y_3),1)}\n")
print(f"Błąd Root Mean Square Logarithmic Error dla model_1: {np.round(root_mean_square_logarithmic_error(y, y_2),1)}")
print(f"Błąd Root Mean Square Logarithmic Error dla model_2: {np.round(root_mean_square_logarithmic_error(y, y_3),1)}\n")
Błąd Mean Absolute Error dla model_1: 0.5
Błąd Mean Absolute Error dla model_2: 0.5
Błąd Root Mean Square Error dla model_1: 0.7
Błąd Root Mean Square Error dla model_2: 0.7
Błąd Root Mean Square Logarithmic Error dla model_1: 0.2
Błąd Root Mean Square Logarithmic Error dla model_2: 0.3
Tak, jak możemy zauważyć na powyższych wynikach, pomimo identycznych błędów MAE oraz RMSE, metryka RMSLE pozwala nam określić, który model byłby lepszy przy naszych założeniach biznsowych. W przypadku zamówień towaru, stworzenie modelu, który częściej będzie niedoszacowywał wartości sprzedażowe spowoduje utracenie sprzedaży w sklepach czego efektem będzie strata sporych sum pieniężnych.
MAPE#
Szczególnym rodzajem metryk są metryki oparte o błędy procentowe. Ich główną zaletą jest fakt, że moga być porównywane pomiędzy modelami niezależnie od jednostki, bądź skali w jakiej predykcja została wykonana ze względu na zastosowanie błędu procentowego. Podstawową metryką jest średni bezwględny błąd procentowy - z ang. Mean Absolute Percentage Error
\(MAPE=\frac{1}{n} \sum^N_{i=1}\frac{|y_i-\hat{y_i}|}{max( \epsilon , |y_i|)}\)
Wartość \(\epsilon\) w mianowniku jest to bardzo niewielka wartość bliska zeru, która pozwala bezpiecznie wyliczyć metryke w momencie, gdy wartość rzeczywista otrzymuje wartość 0.
Ze względu na wyrażenie metryki w ujęciu procentowym metryka ta jest łatwo prównywalna i łatwo zrozumiała.
Jednakże posiada również swoje minus. Kwestia skali i asymetryczności. Dla wartości rzeczywistych bardzo bliskich zeru otrzymujemy wartości ekstremalnie wysokie. Druga kwestia, dużo większą karę nakłada się na przeszacowanie, niż niedoszacowanie. Wynika to z faktu, że dla wartości zbyt niskich nie może wartość błędu przekroczyć 100%. Jednak nie posiada ona granicy dla górnej prognozy. Przez co MAPE faworyzuje modele, które niedoszacowują nad te które przeszacowują.
SMAPE#
W celu poprawy problemu z asymetrią została zaproponowana symetryczna wersja błędu MAPE, czyli SMAPE - z ang. Symetric Mean Absolute Percentage Error
\(SMAPE=\frac{1}{n} \sum^N_{i=1}\frac{|y_i-\hat{y_i}|}{max( \epsilon , \frac{|y_i|+|\hat{y_i}|}{2})}\)
Z zalet więc jest również to metryka wyrażona w wartości procentowej i dodatkowo naprawia wadę asymetryczności wprowadzając dolna granicę 0% i górną 200%.
Ta metryka też ma swoje wady, m.in.: otrzymujemy wartości nieokreślone gdy zarówno wartość rzeczywista i przewidywana są równe 0. Gdy wartość rzeczywista lub prognoza osiągnię wartość 0, to SMAPE automatycznie zwraca górną granicę (to nie koniecznie musi być traktowane jako wada).
Jednakże jest jeszcze jedna ważna różnica, która może okazać się kluczowa w różnych problemach biznesowych. Tak, jak przy wspomnianej wcześniej metryce MSLE kluczowe dla nas jest, aby uniknąć niedoszacowań przy predykcji. Gdy MAPE faworyzowało modele, które niedoszacowują to SMAPE ma efekt odwrotny.
import sys
def mean_absolute_percentage_error(y, y_hat):
"""
Funkcja pozwalająca na wyliczenie wartości Mean Absolute Percentage Error
:param y: wektor wartości rzeczywistych
:param y_hat: wektor wartości przewidywanych
:return: średni bezwględny błąd procentowy na obserwacjach
"""
return np.mean(np.abs(y-y_hat) / np.array([max(sys.float_info.epsilon, x) for x in y]))
def symetric_mean_absolute_percentage_error(y, y_hat):
"""
Funkcja pozwalająca na wyliczenie wartości Symetric Mean Absolute Percentage Error
:param y: wektor wartości rzeczywistych
:param y_hat: wektor wartości przewidywanych
:return: symetryczny średni bezwględny błąd procentowy na obserwacjach
"""
return np.mean(np.abs(y-y_hat) / ((np.abs(y) + np.abs(y_hat))/2))
x = np.array([1,2,3,4,5,6]) # argumenty
y = np.array([2,2,2,2,2,2]) # wartości
y_2 = np.array([2,2,3,3,3,2])
y_3 = np.array([2,2,1,1,1,2])
plt.plot(x,y,'o') # wizualizacja wartości rzeczywistych
plt.plot(x,y_2) # wizualizacja wartości rzeczywistych
plt.plot(x,y_3) # wizualizacja wartości rzeczywistych
plt.legend(['y', 'model_1', 'model_2']) # dodanie legendy
plt.show() # wizualizacja
print(f"Błąd Mean Absolute Error dla model_1: {np.round(mean_absolute_error(y, y_2),1)}")
print(f"Błąd Mean Absolute Error dla model_2: {np.round(mean_absolute_error(y, y_3),1)}\n")
print(f"Błąd Mean Absolute Percentage Error dla model_1: {np.round(mean_absolute_percentage_error(y, y_2),1)}")
print(f"Błąd Mean Absolute Percentage Error dla model_2: {np.round(mean_absolute_percentage_error(y, y_3),1)}\n")
print(f"Błąd Symetric Mean Absolute Percentage Error dla model_1: {np.round(symetric_mean_absolute_percentage_error(y, y_2),1)}")
print(f"Błąd Symetric Mean Absolute Percentage Error dla model_2: {np.round(symetric_mean_absolute_percentage_error(y, y_3),1)}\n")

Błąd Mean Absolute Error dla model_1: 0.5
Błąd Mean Absolute Error dla model_2: 0.5
Błąd Mean Absolute Percentage Error dla model_1: 0.2
Błąd Mean Absolute Percentage Error dla model_2: 0.2
Błąd Symetric Mean Absolute Percentage Error dla model_1: 0.2
Błąd Symetric Mean Absolute Percentage Error dla model_2: 0.3
Ponownie możemy zaobserwować, że metryka SMAPE zwróciła różne od siebie wartości dla zaprezentowanego przypadku bardziej karając model, który niedoszacował wartości predykcji względem wartości rzeczywistych.
Podejście Klasyfikacyjne#
W przypadku klasyfikacji trochę innaczej podchodzimy do oceny jakości modelu. Rodzaj wartości na jakich tutaj operujemy nie są to wartości ciągłe, a znane wcześniej, z góry określone klasy. Na przykład klasyfikując górne części garderoby będzie to zbiór: {‘koszulka’, ‘bluza’, ‘sweter’, ‘koszula’, ‘kurtka’}.
W takim przypadku byłoby ciężko wyliczyczać odległość od wartości prawdziwej i na tej podstawie wyznaczać metryki, ponieważ odległość pomiędzy klasami staje sie tutaj pojęciem abstrakcyjnym, które nie jest naturalnie zdefiniowane.
Z tego powodu, przy klasyfikacji posługujemy się macierzą pomyłek. Macierz ta mówi nam do której klasy została zaklasyfikowana dana obserwacja. Jeśli będzie to błędna predykcja to jesteśmy w stanie wyciągnąć pewne wnioski obserwując z którą inną klasą została zazwyczaj mylona poprawna klasa.
Macierz pomyłek
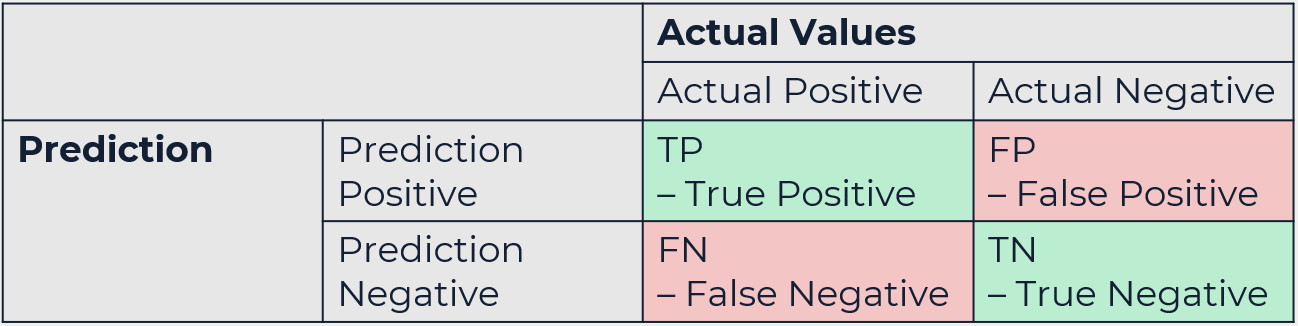
Macierz pomyłek może reprezentować zarówno problem ze zbiorem klas binarnym, bądź wieloklasowy.
W pierwszym przypadku klasyfikator ma za zadanie określić, czy dane zwierzę to kot. Klasy które naturalnie wynikają z tego problemu to ‘Kot’ i ‘nie-Kot’. W związku z dodatkową wiedzą o zbiorze możemy stwierdzić, że jeśli to nie jest ‘Kot’ to to będzie ‘Pies’ i dla podanych poniżej wartości macierze pomyłek prezentuje się w następujący sposób.
Predykcja |
Kot |
Pies |
Kot |
Pies |
Pies |
Pies |
Kot |
Kot |
Pies |
Pies |
Rzeczywista klasa |
Kot |
Kot |
Kot |
Pies |
Kot |
Pies |
Pies |
Kot |
Pies |
Kot |

Drugi przypadek reprezentować będzie klasyfikacje wieloklasową. Taka macierz jest bardziej rozbudowana on macierzy binarnej, jednakże jest dokładnie w taki sam sposób interpretowana.
Predykcja |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
4 |
Rzeczywista klasa |
1 |
4 |
2 |
3 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
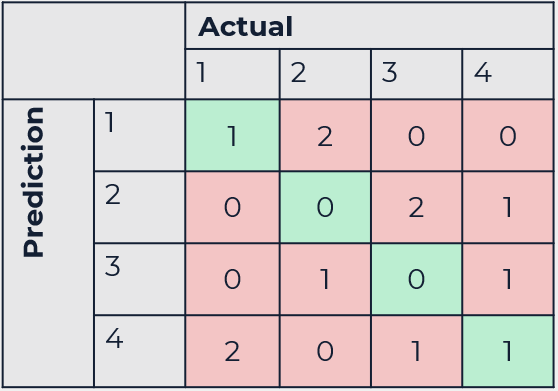
Accuracy - dokładność#
Pierwszą podstawową miarą skuteczności w podejściu klasyfkacyjnym jest dokładność. Miara ta jest wyrażon jako stosunek wszystkkich poprawnie zaklasyfikowanych wartości do wszystkich obserwacj, które podległy klasyfikacji.
\(Accuracy=\frac{TP+TN}{TP+FP+TN+FN}\)
TP to akronim od True Positive, FP od False Positive, TN od True Negative, oraz FN od False Negative.
Metryka ta jest bardzo ogólna i posiada kluczową wadę, a mianowicie przywiązuje jednakową wagę do wartości False Positive oraz False Negative. Nie do końca się to sprawdzi w przypadku niezbalansowanego zbioru danych. W przypadku gdybyśmy posiadali w zbiorze 99% obsewacji należących do klasy ‘A’ oraz 1 % należący do klasy ‘B’ to wykonując zawsze klasyfikacje jako klasa ‘A’ otrzymujemy dokładność na poziomie 99%. Nie do końca jest to poprawnę podejście, a problem się zwiększa ty waga niepoprawnej predykcji nie są jednakowe dla FP oraz FN.
Takim przypadkiem są bardzo rzadkie choroby. Waga jaką przywiązujemy do tego, że niepoprawnie uznamy osobę za zdrową jest znacznie większa, niż gdybyśmy niepoprawnie uznali, że ktoś choruje na daną chorobę. Taką osobę można wysłać na dodatkowe badania, natomiast w przeciwnym przypadku tracimy szansę pomocy chorej osobie. Tak więc jak widać może to być dość kluczowe.
Jeśli chodzi o przypadki medyczne to dla diagnostyki ogólnie bardzo często stosuje się miary Wrażliwości (Sensivity) i Osobliwości (Specificity). Pomagają te miary określić dokładność modelu, którego zadaniem jest informowanie o występowaniu, bądź nieobecności jakiegoś zjawiska.
Specificity#
\(Specificity=\frac{TN}{TN+FP}\)
Miara osobliwości pozwala nam określić, jak często potrafimy poprawnie zaklasyfikować obserwacje w których dane zjawisko nie zachodzi. W przypadku choroby miara ta odpowiada na pytanie: Jak wielu zdrowych ludzi byliśmy w stanie zaklasyfikować jako faktycznie nieposiadających choroby.
Sensitivity / Recall#
\(Sensitivity=\frac{TP}{TP+FN}\)
Miara wrażliwości pozwala nam określić, jak często spośród wszystkich obserwacji, które wskazują na występowanie danego zjawiska jesteśmy w stanie poprawnie określić, że ono występuje. W przypadku choroby miara ta odpowiada na pytanie: Jak wielu chorych byliśmy w stanie zaklasyfikować jako faktycznie chorych.
Miara wrażliwości jest również nazywana w angielskim Recall. Patrząc z perspektywy statystycznej można powiedzieć, że miara ta pozwala lepiej określić dokładność w problemach, gdzie błędy False Negative (czyli błędy II rodzaju) są bardziej krtyczne. Jako przykłady można przytoczyć wymienione wyżje rzadkie choroby, czy oszustwa finansowe, bankowe.
Precision#
\(Precision=\frac{TP}{TP+FP}\)
Miara Recall jest najczęściej zestawiana wraz z miarą Precision, czyli precyzją modelu. Precyzja pozwala nam określić, jak wiele obserwacji z danej klasy udało się zaklasyfikować poprawnie. Pozwala ona lepiej okreslić dokładność w problemach, gdzie błędy False Positive (błąd I rodzaju) są bardziej krytyczne. Takim przypadkiem są na przykład spamy mailowe.
Błąd F-Score#
\(F_1= 2 \times \frac{Precision \times Recall}{Precision + Recall}\)
F1-score jest to metryka, która jest dokładniejszą metryką, niż Accuracy pozwalająca zachować odpowiednia równowagę pomiędzy Recall, a Precision.
W przypadku, gdy potrzebujemy, aby jedna z miar była istotniejsza dla ostatecznego wyniku tej metryki można zastosować bardziej uogólnioną wersję F\(\beta\)-score. W tym przypadku za pomocą współczynnika \(\beta\) możemy zmieniać istotność Precision względem Recall.
\(F_{\beta}=(1+ \beta)^2 \times \frac{Precision \times Recall}{\beta ^2 \times Precision + Recall}\)
ROC Curve#
Kolejną ważną kwestią przy problemach klasyfikacyjnych jest zaznajomienie się z konceptem krzywer ROC. Krzywa ta odzwierciedla relacje pomiędzy wartościami FPR (czyli False Positive Rate), a TPR (czyli True Positive Rate) na przestrzeni różnych thresholds (progi odcięcia / wartości graniczne).
Wartość FPR określamy poprzez wzór:
\(FPR=\frac{FP}{FP+TN}\)
Wartość TPR określamy poprzez wzór:
\(TPR=\frac{TP}{FN+TP}\)
Wartość threshold natomiast jest to wartość graniczna od której uznajemy klasyfikacje do danej klasy. Klasyfikator nie zwraca bezpośrednio informacji na temat tego, że jest to konkretna klasa, a bardziej prawdopodobieństwo, że dana obserwacja może zostać zaklasyfikowana do danej klasy.
I tak przyjmując, że klasyfikator tego czy dane zdjęcie przedstawia kota zwraca nam wartości:
Lp. |
Prawdopodobieństwo |
|---|---|
0 |
0.3 |
1 |
0.45 |
2 |
0.6 |
3 |
0.8 |
Jeśli określimy wartość threshold na 50%, to oznacza, że jeśli klasyfikator powyżej 50% powie nam, że to może być ‘Kot’ to to nam wystarcza, aby zaklasyfikować daną obserwację jako ‘Kot’. W taki sposób można sterować dokładnością modelu.
Lp. |
Prawdopodobieństwo |
Threshold 1 |
Klasyfikacja 1 |
Threshold 2 |
Klasyfikacja 2 |
Threshold 3 |
Klasyfikacja 3 |
|---|---|---|---|---|---|---|---|
0 |
0.3 |
0.2 |
Kot |
0.5 |
nie-Kot |
0.7 |
nie-Kot |
1 |
0.45 |
0.2 |
Kot |
0.5 |
nie-Kot |
0.7 |
nie-Kot |
2 |
0.6 |
0.2 |
Kot |
0.5 |
Kot |
0.7 |
nie-Kot |
3 |
0.8 |
0.2 |
Kot |
0.5 |
Kot |
0.7 |
Kot |
Manipulując wartością threshold otrzymujemy inne końcowe etykiety i tą zmianę przedstawia krzywa ROC pozwalając nam ustalić jaki próg odcięcia będzie dla nas najbardziej korzystny. ROC curve to wartości TPR oraz FPR przedstawione na wykresie dla różnych wartości theshold.
I tak cofając się do nasze pierwszego przypadku:
Predykcja |
Kot |
Pies |
Kot |
Pies |
Pies |
Pies |
Kot |
Kot |
Pies |
Pies |
Rzeczywista klasa |
Kot |
Kot |
Kot |
Pies |
Kot |
Pies |
Pies |
Kot |
Pies |
Kot |
import pandas as pd
from prettytable import PrettyTable
from sklearn.metrics import confusion_matrix
from sklearn.metrics import roc_curve
y = ['Kot', 'Kot', 'Kot', 'Pies', 'Kot', 'Pies', 'Pies', 'Kot', 'Pies' ,'Kot'] # wartości oczekiwana
y = np.array([int(y_n=='Kot') for y_n in y]) # rzutowanie na {0,1} = {'nieKot', 'Kot'}
probabilities = np.array([0.75, 0.31, 0.69, 0.42, 0.54, 0.36, 0.78, 0.82, 0.11, 0.49]) # Prawdopodobieństwo z modelu
predictions = np.array([int(prob>=0.6) for prob in probabilities])
conf_matrix = confusion_matrix(y, predictions)
print("Return z funkcji sklearn.metrics.confusion_matrix: ")
print(conf_matrix)
print()
confusion_matrix_t = PrettyTable(['', 'Prediction_True', 'Prediction_False'])
confusion_matrix_t.add_row(['Actual_True']+list(conf_matrix[0]))
confusion_matrix_t.add_row(['Actual_False']+list(conf_matrix[1]))
print("Ładniejsza forma reprezentacji wartości")
print(confusion_matrix_t)
print("\n Wyliczenie poszczególnych metryk \n")
TP = conf_matrix[0][0]
FP = conf_matrix[1][0]
TN = conf_matrix[1][1]
FN = conf_matrix[0][1]
print(f"True Positive: {TP}")
print(f"False Positive: {FP}")
print(f"True Negative: {TN}")
print(f"False Negative: {FN}\n")
# Accuracy
print(f"Accuracy: {(TP+TN)/(TP+TN+FP+FN)}")
# Specificity
print(f"Specificity: {(TN)/(TN+FP)}")
# Sensitivity/Recall
Recall = (TP)/(TP+FN)
print(f"Sensitivity/Recall: {(TP)/(TP+FN)}")
# Precision
Precision = (TP)/(TP+FP)
print(f"Precision: {(TP)/(TP+FP)}")
# F-score
print(f"F1-score: {2* (Precision * Recall)/(Precision + Recall)}")
print(f"F_0.5-score: {(1+np.power(0.5,2))* (Precision * Recall)/((np.power(0.5,2) * Precision) + Recall)}")
print(f"F_2-score: {(1+np.power(2,2))* (Precision * Recall)/((np.power(2,2) * Precision) + Recall)} \n")
print("\n Krzywa ROC Curve \n")
fpr, tpr, thresholds = roc_curve(y, probabilities) # użycie funkcji z biblioteki sklearn
def plot_static_roc_curve(fpr, tpr):
"""
Wizaulizacja krzywej ROC
"""
plt.figure(figsize=[7,7])
plt.fill_between(fpr, tpr, alpha=.5)
plt.plot([0,1], [0,1], linestyle=(0, (5, 5)), linewidth=2)
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("ROC curve");
plot_static_roc_curve(fpr, tpr) # użycie funkcji wizualizującej
Return z funkcji sklearn.metrics.confusion_matrix:
[[3 1]
[3 3]]
Ładniejsza forma reprezentacji wartości
+--------------+-----------------+------------------+
| | Prediction_True | Prediction_False |
+--------------+-----------------+------------------+
| Actual_True | 3 | 1 |
| Actual_False | 3 | 3 |
+--------------+-----------------+------------------+
Wyliczenie poszczególnych metryk
True Positive: 3
False Positive: 3
True Negative: 3
False Negative: 1
Accuracy: 0.6
Specificity: 0.5
Sensitivity/Recall: 0.75
Precision: 0.5
F1-score: 0.6
F_0.5-score: 0.5357142857142857
F_2-score: 0.6818181818181818
Krzywa ROC Curve
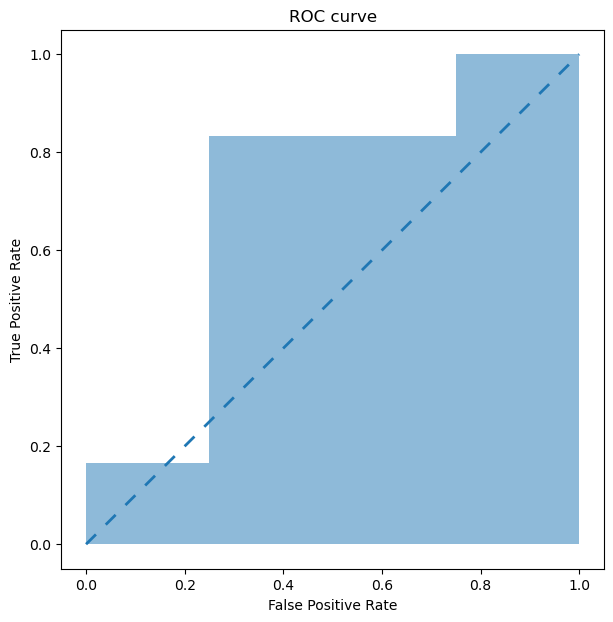
AUC metric#
Obszar znajdujący się pod krzywą ROC nazywany jest błędem AUC i jest to miara wydajności klasyfikatora dla wszystkich wartości progowych. Metryka ta przyjmuje wartości z zakresu od 0 do 1, gdzie wartożsci bliższe 1 oznacza, że krzywa ROC zbliża się ku lewemu górnemu narożnikowi wykresu.
Wartość tą interpretujemy, że dla wysokiej wartości AUC model oceni wyżej losowy pozytywny przypadek, niż losowy negatywny dla klasyfikacji w danej klasie.
Podejście Grupujące#
Grupowanie, czyli szerzej znane jako klasteryzacja (od ang. “Clustering”) polega na podzieleniu populacji lub próbki na wiele grup, tak aby obserwacje w tych samych grupach były bardziej podobne do obserwacji w tej samej grupie, niż w innej.
V-measure#
Metryka ta łączy dwa koncepty Jednorodności (Homogeneity) oraz Kompletności (Completeness).
Metryka ta przyjmuje wartości od 0 do 1, gdzie 1 oznacza najlepszą jakość w obrębie tej metryki. Jednym z minusów dla tej metryki jest konieczność posiadania wiedzy na temat prawdziwych klastrów (grup) dla danych obserwacji, a często przy problemach klastrowania nie znamy tych grup i chcemy je wywnioskować na podstawie wyników algorytmu.
Jednorodność - każdy klaster zawiera tylko członków jednej klasy
\(h=1- \frac{H(C|K)}{H(C)}\)
, gdzie
\(H(C|K)=-\sum _{c,k} \frac{n_{ck}}{N}log \frac{n_{ck}}{n_k}\)
Wartości \(n_{ck}\) - oznacza ilość obserwacji klasy c w obrębie klastra k, natomiast \(n_k\) - oznacza ilość wszystkich obserwacji w obrębie klastra k.
from sklearn.metrics.cluster import v_measure_score
import matplotlib.patches as patches
# stworzenie prostej przykladowej ramki danych
df_completness = pd.DataFrame({'klasa':[1,1,1,1,1,1,1,1,2,2,2,2,3,3,3,3],
'x':[0.2,0.3,0.15,0.24,0.14,0.32,0.4,0.2,0.64,0.74,0.69,0.71,0.89,0.94,0.76,0.83],
'y':[0.1,0.2,0.12,0.11,0.64,0.76,0.68,0.66,0.45,0.62,0.53,0.55,0.1,0.12,0.08,0.16]})
print("Homogeneity - każdy Klaster posiada obserwacje tylko z jednej klasy.")
fig, ax = plt.subplots()
scatter = ax.scatter(df_completness.x, df_completness.y, c=df_completness.klasa) # Wizualizacjach obserwacji
ax.add_artist(ax.legend(*scatter.legend_elements(), loc="upper right", title="Klasy")) # dodanie legendy
ax.add_patch(patches.Rectangle((0.11,0.05), 0.32, 0.3, fill=False)) # dodanie oznaczenia klastra 1
ax.text(0.15,0.3,"Klaster 1")
ax.add_patch(patches.Rectangle((0.11,0.55), 0.32, 0.3, fill=False)) # dodanie oznaczenia klastra 2
ax.text(0.15,0.8,"Klaster 2")
ax.add_patch(patches.Rectangle((0.58, 0.4), 0.2, 0.3, fill=False)) # dodanie oznaczenia klastra 3
ax.text(0.6,0.65,"Klaster 3")
ax.add_patch(patches.Rectangle((0.7,0.05), 0.3, 0.2, fill=False)) # dodanie oznaczenia klastra 4
ax.text(0.72,0.2,"Klaster 4")
plt.show()
Homogeneity - każdy Klaster posiada obserwacje tylko z jednej klasy.
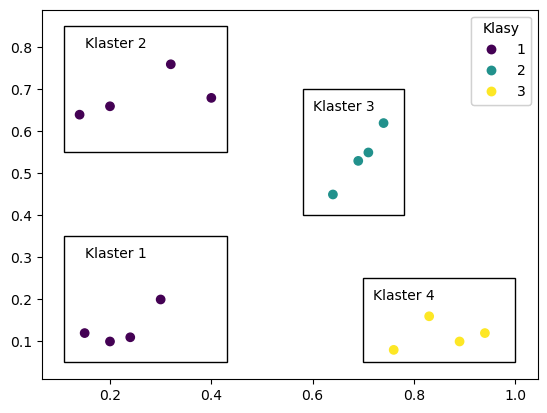
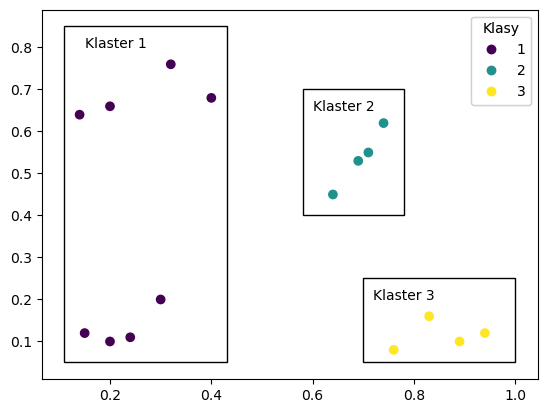
Kompletność - wszyscy członkowie danej klasy są przypisani do tego samego klastra
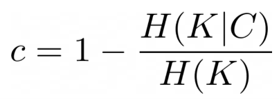
from sklearn.metrics.cluster import v_measure_score
import matplotlib.patches as patches
# stworzenie prostej przykladowej ramki danych
df_completness = pd.DataFrame({'klasa':[1,1,1,1,1,1,1,1,2,2,2,2,3,3,3,3],
'x':[0.2,0.3,0.15,0.24,0.14,0.32,0.4,0.2,0.64,0.74,0.69,0.71,0.89,0.94,0.76,0.83],
'y':[0.1,0.2,0.12,0.11,0.64,0.76,0.68,0.66,0.45,0.62,0.53,0.55,0.1,0.12,0.08,0.16]})
print("Completeness - każdy Klaster posiada obserwacje tylko z jednej klasy.")
fig, ax = plt.subplots()
scatter = ax.scatter(df_completness.x, df_completness.y, c=df_completness.klasa) # Wizualizacjach obserwacji
ax.add_artist(ax.legend(*scatter.legend_elements(), loc="upper right", title="Klasy")) # dodanie legendy
ax.add_patch(patches.Rectangle((0.11,0.05), 0.32, 0.8, fill=False)) # dodanie oznaczenia klastra 1
ax.text(0.15,0.8,"Klaster 1")
ax.add_patch(patches.Rectangle((0.58, 0.4), 0.2, 0.3, fill=False)) # dodanie oznaczenia klastra 2
ax.text(0.6,0.65,"Klaster 2")
ax.add_patch(patches.Rectangle((0.7,0.05), 0.3, 0.2, fill=False)) # dodanie oznaczenia klastra 3
ax.text(0.72,0.2,"Klaster 3")
plt.show()
Completeness - każdy Klaster posiada obserwacje tylko z jednej klasy.
Silhouette Coefficient#
Współczynnik ten określa, jak bardzo klastry są od siebie oddalone oraz rozróżnialne. Przyjmuje on wartości od -1 do 1, gdzie:
1 - Klastry są od siebie oddalone i łatwo rozróżnialne
0 - Klastry są przeciętne, odległość między nimi jest nieznacząca
-1 - Klastry zostały źle przypisane
Wzór określający ten współczynnik przedstawia się następująco:
, gdzie
\(a\) - jest to średnia odległość pomiędzy obserwacją, a pozostałymi obserwacjami w danym klastrze
\(b\) - jest to średnia odległość pomiędzy obserwacją, a pozostałymi obserwacjami w kolejnym najbliższym klastrze
Po zebraniu wartości dla wszystkich obserwacj wartość ta jest uśredniana.
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
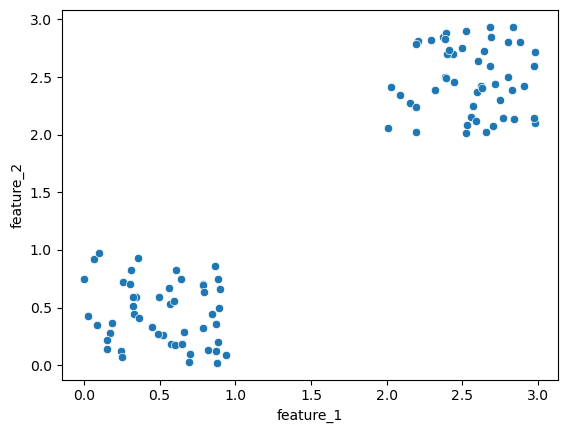
first_group = np.random.rand(50,2) # pierwszy klaster
second_group = np.random.rand(50,2) + 2 # drugi klaster przesuniety
data_set = np.concatenate((first_group,second_group)) # zbiór danych
df_data = pd.DataFrame(data_set, columns=['feature_1', 'feature_2']) # wygodniejsze przedstawienie danych
sns.scatterplot(df_data, x='feature_1', y='feature_2') # wizualizacja danych
plt.show()
KMean_model = KMeans(n_clusters=2) # inicjalizacja modelu klastrującego na 2 klastry
KMean_model.fit(df_data) # dopasowanie się do danych
labels = KMean_model.predict(df_data) # dokonanie podziału na klastry
display(df_data)
print(f"Silhouette Score (liczba klastrow n=2): {silhouette_score(df_data, labels)}") # obliczenie wartości wspolczynnika Silhouette
sns.scatterplot(data = df_data,hue=labels, x='feature_1', y='feature_2') # wizualizacja podziału na klastry
plt.show()
KMean_model = KMeans(n_clusters=3) # inicjalizacja modelu klastrującego na 3 klastry
KMean_model.fit(df_data) # dopasowanie się do danych
labels = KMean_model.predict(df_data) # dokonanie podziału na klastry
print(f"Silhouette Score (liczba klastrow n=3): {silhouette_score(df_data, labels)}") # obliczenie wartości wspolczynnika Silhouette
sns.scatterplot(df_data,hue=labels, x='feature_1', y='feature_2') # wizualizacja podziału na klastry
plt.show()
| feature_1 | feature_2 | |
|---|---|---|
| 0 | 0.309465 | 0.824680 |
| 1 | 0.869060 | 0.857130 |
| 2 | 0.247198 | 0.125108 |
| 3 | 0.569563 | 0.529739 |
| 4 | 0.067738 | 0.918478 |
| ... | ... | ... |
| 95 | 2.440729 | 2.453220 |
| 96 | 2.390453 | 2.491654 |
| 97 | 2.569401 | 2.247919 |
| 98 | 2.972058 | 2.147259 |
| 99 | 2.499744 | 2.749131 |
100 rows × 2 columns
Silhouette Score (liczba klastrow n=2): 0.8252728341898338
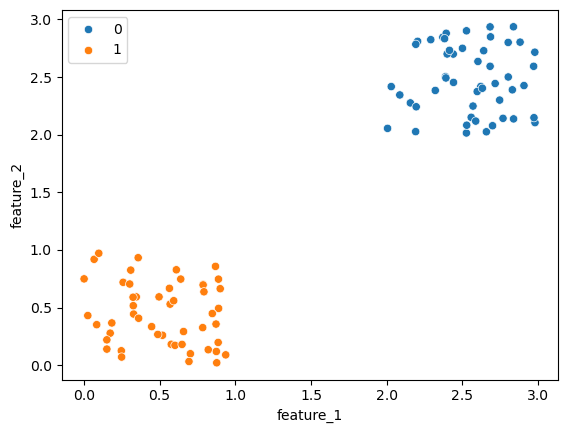
Silhouette Score (liczba klastrow n=3): 0.5903118185865727
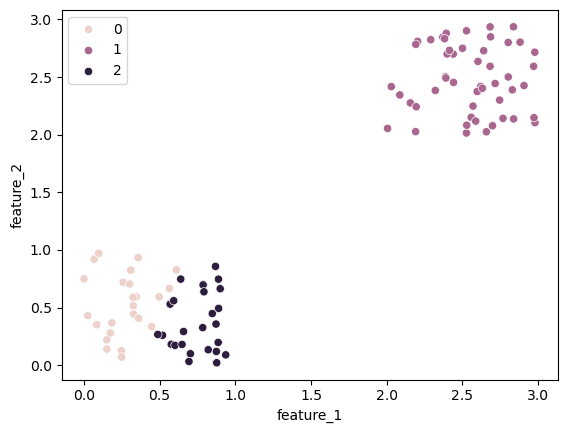
Jak można zaobserwować wartość Silhouette Coefficient (Score) jest niższa w przypadku, gdy liczba wybranych przez nas klastrów wynosi 3, gdyż klastry są mniej rozróżnialne.
Jest to dodatkowe zastosowanie również tej metryki. Dzięki niej możemy okreslić jaka liczba klastrów dla naszego zbioru danych będzie optymalna.
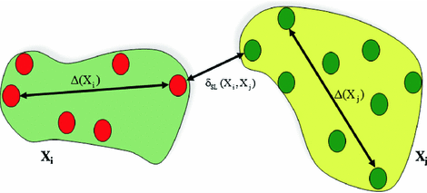
Dunn’s Index#
Ostatnią omawianą metryką dla problemów grupowania jest metryka Dunn’s Index.
Index ten jest równy minimalnej odległości między klsatrami podzielonej przez maksymalny rozmiar tego klastra.
\(DI(C)=\frac{\min_{c_k \in C}{\delta(c_k, c_l)}}{\max_{c_k\in C}\Delta(c_k)}\)
Duże odległości pomiędzy klastrami są przejawem lepszej separacji, natomiast mniejszy rozmiar klastra świadczy o wyższej gęstości klastra. Jeśli obie z tych cech zostaną odpowiednio usatysfakcjonowane będzie to prowadziło do wyższej wartości DI (Dunn’s Index). Wyższe DI oznacza lepsze grupowanie pod warunkiem, że lepsze grupowanie jest zdefiniowane jako zwarte klastry dobrze oddzielone od siebie nawzajem.