Wizualizacja danych w Python

Wizualizacja danych w Python#

Odpytanie bazy z poziomu kodu#

W odpowiednich miejscach należy uzupełnić prawidłowymi danymi (user, password, host, port, database, query)

import pandas as pd
import sqlalchemy as sa

user = ""
password = ""

if user:
    connection_url = sa.engine.url.URL.create(
        "mssql+pyodbc",
        host="127.0.0.1,0000", # port after comma
        username=user,
        password=password,
        database="database",
        query=dict(driver="ODBC Driver 17 for SQL Server")
    )
    engine = sa.create_engine(connection_url, fast_executemany=True)


    query = """
    SELECT
        *
    FROM
        [database].[dataset].[table]
    """

    df = pd.read_sql(sa.text(query), engine.connect())

    df.head()
else:
    print("Uzupełnij dane logowania.")

Uzupełnij dane logowania.

Wstęp#

Cykl życia projektów Data Science składa się z różnych elementów. Jednym z nich jest etap Exploratory Data Analysis , a więc Eksploracyjna Analiza Danych. Jego celem jest przeprowadzenie zaawansowanej analizy statystycznej opierając sie nie tylko na statystykach opisowych, ale również na dobrze dobranych wizualizacjach. Stąd przygotowanie dobrej analizy nie jest możliwe bez umiejętności wizualizacji danych oraz prawidłowej ich interpretacji.

Istnieje wiele rodzajów wizualizacji danych. Wszystko zależy od tego jakiego rodzaju dane posiadamy - kategoryczne, numeryczne, a może dane zależne od czasu. Każda z metod wizualizacji odpowie nam na inne pytanie, dlatego dobranie odpowiedniej do naszego problemu jest kluczowe w kontekście zrozumienia danych przez nas, jak i naszych kolegów z zespołu czy kierownictwo.

Poniższy Tutorial opiera się na trzech najczęściej wykorzystywanych bibliotekach do wizualizacji danych w Python: matplotlib, seaborn oraz plotly. Są to najczęściej wykorzystywane przez nas biblioteki w trakcie trwania projektu. Ich opanowanie jest często kluczowe w kontekście przygotowania dobrej jakości analizy. W naszym odczuciu opanowanie przynajmniej podstaw każdej z tych bibiliotek może zapewnić zbudowanie ciekawej analizy, która odpowie nam na postawione przez nas pytanie. Oczywiście musicie mieć na uwadze, że nie wyczerpują one pełnej gamy dostępnych bibliotek czy metod wizualizacjii danych.

Wnioski:

Wizualizacja danych jako niezbędny element Eksploracyjnej Analizy Danych.
Dobra wizualizacja to klucz do sukcesu i prawidłowego zrozumienia danych.

Biblioteki#

Zadanie 0

Do poniższego Tutorialu niezbędne będzie utworzenie środowiska.

Utwórz środowisko z wersją pythona 3.10 i zainstaluj na nim następujące biblioteki:

scikit-learn
pandas
numpy
seaborn
matplotlib
plotly
ipykernel
pyodbc
sqlalchemy
nbformat
statsmodels

Podpowiedź znajdziesz w pierwszym tutorialu JupyterLab & Anaconda.

# Pobranie przykladowych danych
from sklearn.datasets import fetch_california_housing

# Data wrangling 
import pandas as pd
import numpy as np

# Data visualization
import seaborn as sns
from matplotlib import pyplot as plt
from plotly import express as px
import plotly.graph_objects as go

# Inne
import datetime as dt

Przygotowanie danych#

Do przygotowania wizualizacji posłużą nam dane dostępne w sklearn.datasets oraz seaborn.datasets.

Housing#

Opis: Zestaw danych California Housing zawiera informacje ze spisu powszechnego w Kalifornii z 1990 roku.

Dane nie są w żaden sposób wyczyszcone, stąd posłużą jako dobry materiał do eksploracyjnej analizy danych.

# Funkcja do przygotowania ramki danych
def data_preparation():
    """Przygotowanie danych na potrzeby notatnika."""
    
    # Load data
    housing = fetch_california_housing()
    
    # Data Array
    df_array = housing.data.copy()
    target = housing.target.copy()
    target = target.reshape(len(target), 1)
    
    df_array = np.concatenate([df_array, target], axis=1)
    
    # Colnames
    colnames = housing.feature_names.copy()
    colnames.append(housing.target_names[0])
    
    # Data Frame
    df = pd.DataFrame(df_array, columns=colnames)
    
    return df

# Pobranie danych

# Housing
housing = data_preparation()

print(f'Wymiar ramki danych: {housing.shape}')
print(f'Nazwy kolumn: {housing.columns.values}')

Wymiar ramki danych: (20640, 9)
Nazwy kolumn: ['MedInc' 'HouseAge' 'AveRooms' 'AveBedrms' 'Population' 'AveOccup'
 'Latitude' 'Longitude' 'MedHouseVal']

# Wyswietlenie pierwszych 5 obserwacji
housing.head()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude	MedHouseVal
0	8.3252	41.0	6.984127	1.023810	322.0	2.555556	37.88	-122.23	4.526
1	8.3014	21.0	6.238137	0.971880	2401.0	2.109842	37.86	-122.22	3.585
2	7.2574	52.0	8.288136	1.073446	496.0	2.802260	37.85	-122.24	3.521
3	5.6431	52.0	5.817352	1.073059	558.0	2.547945	37.85	-122.25	3.413
4	3.8462	52.0	6.281853	1.081081	565.0	2.181467	37.85	-122.25	3.422

housing.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 9 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   MedInc       20640 non-null  float64
 1   HouseAge     20640 non-null  float64
 2   AveRooms     20640 non-null  float64
 3   AveBedrms    20640 non-null  float64
 4   Population   20640 non-null  float64
 5   AveOccup     20640 non-null  float64
 6   Latitude     20640 non-null  float64
 7   Longitude    20640 non-null  float64
 8   MedHouseVal  20640 non-null  float64
dtypes: float64(9)
memory usage: 1.4 MB

Niektóre z tych zmiennych poddamy transformacji do celów edukacyjnych.

# Data transformation
housing['AveRooms'] = housing['AveRooms'].astype(int)
housing['AveBedrms'] = housing['AveBedrms'].astype(int)

# Feature Engineering
housing['AveRooms_greater_5'] = np.where(housing['AveRooms'] > 5, '>5', '<=5')
housing['MedInc_greater_5'] = np.where(housing['MedInc'] > 5, '>5', '<=5')

housing.head()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude	MedHouseVal	AveRooms_greater_5	MedInc_greater_5
0	8.3252	41.0	6	1	322.0	2.555556	37.88	-122.23	4.526	>5	>5
1	8.3014	21.0	6	0	2401.0	2.109842	37.86	-122.22	3.585	>5	>5
2	7.2574	52.0	8	1	496.0	2.802260	37.85	-122.24	3.521	>5	>5
3	5.6431	52.0	5	1	558.0	2.547945	37.85	-122.25	3.413	<=5	>5
4	3.8462	52.0	6	1	565.0	2.181467	37.85	-122.25	3.422	>5	<=5

Przed przystąpieniem do wizualizacji należy zaznaczyć, które z powyższych zmiennych to zmienna celu, a które to zmienne objaśniające.

Zmienna celu: MedHouseVal

Zmienne objaśniające: MedInc, HouseAge, AveRooms, AveBedrms, Population, AveOccup, Latitude, Longitude

Fmri#

Opis: Funkcjonalne obrazowanie rezonansem magnetycznym lub funkcjonalny MRI (fMRI) mierzy aktywność mózgu za pomocą silnego, statycznego pola magnetycznego w celu wykrycia zmian związanych z przepływem krwi. Kiedy używany jest obszar mózgu, przepływ krwi do tego obszaru również wzrasta. Zwiększony przepływ krwi jest reprezentowany przez sygnał o wyższej amplitudzie, postrzegany jako silna aktywność nerwowa.

## Fmri
fmri = sns.load_dataset("fmri")

print(f'Wymiar ramki danych: {fmri.shape}')
print(f'Nazwy kolumn: {fmri.columns.values}')

Wymiar ramki danych: (1064, 5)
Nazwy kolumn: ['subject' 'timepoint' 'event' 'region' 'signal']

fmri.head()

	subject	timepoint	event	region	signal
0	s13	18	stim	parietal	-0.017552
1	s5	14	stim	parietal	-0.080883
2	s12	18	stim	parietal	-0.081033
3	s11	18	stim	parietal	-0.046134
4	s10	18	stim	parietal	-0.037970

W tym przypadku mamy do czynienia z pewnymi szeregami czasowymi, gdzie zmienna czasu jest timepoint, a zmienna celu signal. Szeregi czasowe możemy podzielić względem zmiennej region oraz event, gdzie region == parietal dotyczy płatu ciemieniowego, natomimast region == frontal dotyczy jego płatu czołowego mózgu.

Tips#

Opis: Ramka danych opierająca się na informacjach reprezentujących niektóre dane dotyczące napiwków, w których jeden kelner zapisał informacje o każdym napiwku, który otrzymał w ciągu kilku miesięcy pracy w jednej restauracji. Kelner zebrał kilka zmiennych: napiwek w dolarach, rachunek w dolarach, płeć płatnika rachunku, czy na imprezie byli palacze, dzień tygodnia, pora dnia i wielkość imprezy.

## Tips
tips = sns.load_dataset("tips")

print(f'Wymiar ramki danych: {tips.shape}')
print(f'Nazwy kolumn: {tips.columns.values}')

Wymiar ramki danych: (244, 7)
Nazwy kolumn: ['total_bill' 'tip' 'sex' 'smoker' 'day' 'time' 'size']

tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

W tym przypadku możemy ustalić następujące zmienne objaśniające oraz zmienną celu:

Zmienna celu: tip

Zmienne objaśniające: total_bill, sex, smoker, day, time, size

Anscombe#

Opis: Kwartet Anscombe’a to cztery zestawy danych o identycznych cechach statystycznych, takich jak średnia arytmetyczna, wariancja, współczynnik korelacji czy równanie regresji liniowej, jednocześnie wyglądających zgoła różnie przy przedstawieniu graficznym. Układ tych danych został stworzony w 1973 roku przez brytyjskiego statystyka Francisa Anscombe’a aby ukazać znaczenie graficznej reprezentacji danych przy okazji ich analizy statystycznej.

## Anscombe
anscombe = sns.load_dataset("anscombe")

print(f'Wymiar ramki danych: {anscombe.shape}')
print(f'Nazwy kolumn: {anscombe.columns.values}')

Wymiar ramki danych: (44, 3)
Nazwy kolumn: ['dataset' 'x' 'y']

anscombe.head()

	dataset	x	y
0	I	10.0	8.04
1	I	8.0	6.95
2	I	13.0	7.58
3	I	9.0	8.81
4	I	11.0	8.33

Poniżej, dowód dotyczących tych samych wartości statystyki średniej arytmetycznej oraz odchylenia standardowego dla zmiennych x i y.

anscombe.groupby(['dataset']).agg({
    'x': ['mean', 'std', 'min', 'max'],
    'y': ['mean', 'std', 'min', 'max']
})

	x				y
	mean	std	min	max	mean	std	min	max
dataset
I	9.0	3.316625	4.0	14.0	7.500909	2.031568	4.26	10.84
II	9.0	3.316625	4.0	14.0	7.500909	2.031657	3.10	9.26
III	9.0	3.316625	4.0	14.0	7.500000	2.030424	5.39	12.74
IV	9.0	3.316625	8.0	19.0	7.500909	2.030579	5.25	12.50

Wizualizacja zależności statystycznych#

Analiza statystyczna to proces zrozumienia, w jaki sposób zmienne w zbiorze danych są ze sobą powiązane i jak te relacje zależą od innych zmiennych. Wizualizacja może być kluczowym elementem tego procesu, ponieważ gdy dane są odpowiednio wizualizowane, możemy dostrzec trendy i wzorce wskazujące na związek między nimi. Przeprowadzenie dokładnej analizy statystycznej jest procesem często niezbędnym w pierwszej fazie projektu, gdyd dobre zrozumienie danych jest kluczowe przed przystąpieniem do dalszych etapów projektu.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme(style="darkgrid")

Badanie relacji między zmiennymi przy użyciu wykresu punktowego#

Wykres punktowy jest podstawą wizualizacji statystycznej. Pozwala nam odpowiedzieć na kilka podstwowych pytań:

- Czy istnieje jakakolwiek zależność między dwiema zmiennymi?
- Czy istnieją obserwacje nietypowe (anomalie)?
- Czy dane układają nam się może w jakieś podgrupy?

Oczywiście to tylko przykłady. Generalnie, wykres punktowy przedstawia łączny rozkład dwóch zmiennych za pomocą punktów, gdzie każdy punkt reprezentuje obserwacje w zbiorze danych. Wykres tego rodzaju umożliwia wywnioskowanie czy istnieje między zmiennymi jakakolwiek relacja - liniowa bądź nieliniowa. Na podstawie odnalezionych relacji możemy też dojść do pierwszych wniosków związanych z przyszłym etapem Feature Engineering - może się okazać, że transformacja zmiennej objaśnianej np. log, power, square itp. w lepszy sposób wyjaśnia naszą zmienną celu.

sns.relplot(x="MedInc", y="MedHouseVal", data=housing, alpha=0.3)
plt.title('Wykres punktowy', fontsize=18)

Text(0.5, 1.0, 'Wykres punktowy')

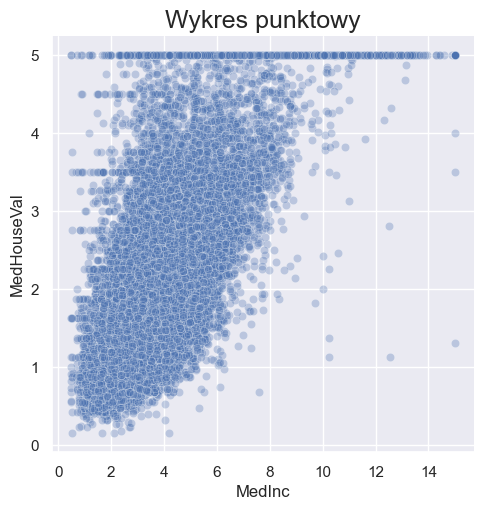
../_images/3f95524c8948900ff4661d6752bdc5dc2a4d8e0c2856e6c5a3ee4c6489a37880.png

Info

W wielu rodzajach wizualizacji pojawia sie parametr alpha. Służy on do ustawienia przezroczystosci wykresu. Zdefiniowanie tego parametru jest szczególnie przydatne, gdy wiele obserwacji nachodzi na siebie. Dzięki ustawieniu niskiej wartości alpha jesteśmy w stanie określić w jakim obszarze najczęściej występują nasze dane.

W przypadku biblioteki matplotlib wykres wyglądał by następująco:

plt.scatter(x=housing['MedInc'], y=housing['MedHouseVal'], alpha=0.3)
plt.xlabel('MedInc')
plt.ylabel('MedHouseVal')
plt.title('Wykres punktowy', fontsize=18)

Text(0.5, 1.0, 'Wykres punktowy')

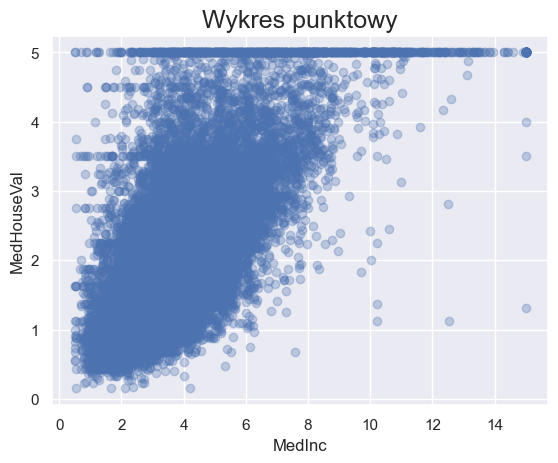
../_images/21af90a2e7c674fa223a23bc959f3e73e86899db12dcb8dbd2455fcd3f5862d1.png

Info

Z uwagi na to, że pod spodem biblioteki seaborn działa matplotlib to wiele funkcji, działająych dla matplotlib tj. xlabel, ylabel, title działa również dla seaborn.

W przypadku biblioteki seaborn w prosty sposób można dodać dodatkową relację do tego rodzaju wykresu. Dodając parameter hue, mamy możliwość sprawdzić powyższą relację względem zmiennej kategorycznej.

sns.relplot(x="MedInc", y="MedHouseVal", hue="AveRooms_greater_5", data=housing)

<seaborn.axisgrid.FacetGrid at 0x20b966c2030>

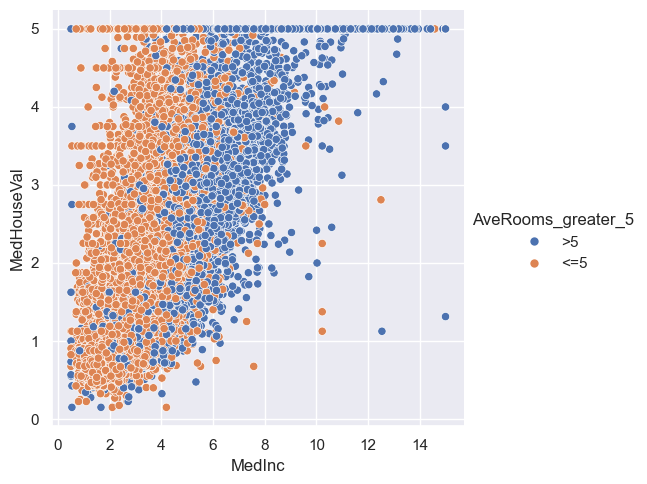
../_images/280f1d0bf2372f13e091f0b447df78b910bcadf1675140c3613169441396a95b.png

Aby sprawdzić kolejną relację, mamy możliwość dodania zmiennej kategorycznej która będzie charakteryzowała się innym znacznikiem - do tego służy parametr style.

sns.relplot(x="MedInc", y="MedHouseVal", hue="AveRooms_greater_5", style="MedInc_greater_5", data=housing)

<seaborn.axisgrid.FacetGrid at 0x20b98020650>

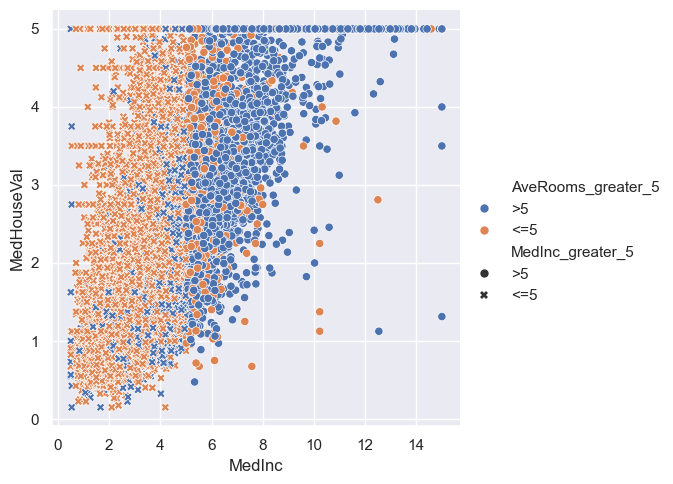
../_images/370df1ba783eb78cfed88e57d29142ac2b3a4827337545da9f7230bf4c245e7e.png

Na powyższych wykresach w parametrach hue oraz style podane są zmienne kategoryczne. W przypadku podania tam zmiennych numerycznych wizualizacja wyglądała by następująco.

sns.relplot(x="MedInc", y="MedHouseVal", hue="HouseAge", data=housing)

<seaborn.axisgrid.FacetGrid at 0x20b981faf00>

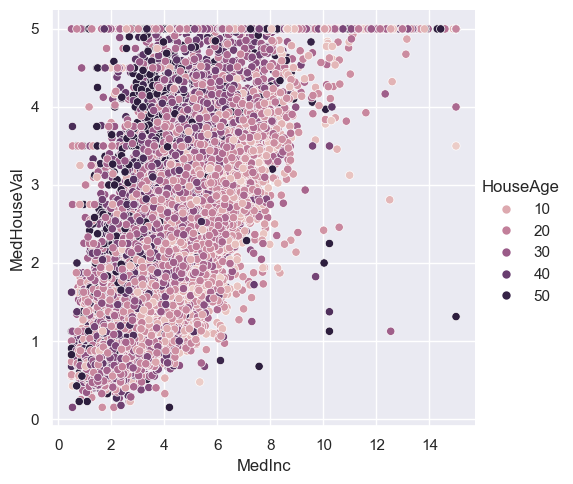
../_images/35ef3d60483410d1cfff937b8263bd5991505c9ae601d08764084be4dc71f9b2.png

ha_value = np.sort(housing['HouseAge'].unique())

print(f'Unikalne wartości HouseAge: {ha_value}')

Unikalne wartości HouseAge: [ 1.  2.  3.  4.  5.  6.  7.  8.  9. 10. 11. 12. 13. 14. 15. 16. 17. 18.
 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36.
 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52.]

Jak widać funkcja relplot sama poradziła sobie z podziałem naszej zmiennej tak, aby kolory punktów nie były przypisane do każdej z wartości tylko do ich przedziałów - w tym przypadku do przedziału długości 10 jednostek.

Bardzo często podczas pracy z danymi chcemy mieć możliwość pracy interaktywnej z naszymi danymi - w tym przypadku bardzo pomocny jest pakiet plotly.

fig = px.scatter(
    housing,
    x="MedInc",
    y="MedHouseVal",
    color="AveRooms_greater_5",
    symbol="MedInc_greater_5",
    opacity=0.5
)
fig.show()

Plotly jest w pełni modyfikowalne

fig = px.scatter(
    housing,
    x="MedInc",
    y="MedHouseVal",
    color="AveRooms_greater_5",
    symbol="MedInc_greater_5",
    opacity=0.7
)

symbol_styles = {
    ">5":  dict(symbol="diamond", line=dict(width=2, color="black"), size=10),
    "<=5": dict(symbol="x", line=dict(width=2, color="white"), size=10),
}

for trace in fig.data:
    _, symbol_cat = trace.name.split(", ")
    if symbol_cat in symbol_styles:
        trace.marker.update(**symbol_styles[symbol_cat])

fig.show()

Podkreślenie relacji liniowych między zmiennymi#

Choć wykresy punktowe są bardzo efektywne i same w sobie są w stanie bardzo dużo powiedzieć nam o relacjach między zmiennymi to nie są jednak uniwersalnym typem wykresu. Wizualizacja powinna być dostosowana do specyfiki analizowanych danych i pytania, na które próbujemy sobie odpowiedzieć.

W przypadku szeregów czasowych chcemy zrozumieć zmiany ciągłej zmiennej w stosunku do zmiennej czasu. W takiej sytuacji niezbędnym jest narysowanie wykresu liniowego.

Wykresy liniowe sprawdzają się gdy naszym celem jest wizualizacja szeregu czasowego lub sprawdzenie ostatecznej zależności liniowej między zmiennymi - jak w przypadku regplot powyżej.

W poniższym przykładzie przed przystąpieniem do takiej wizualizacji należy przygotować dane.

import datetime as dt

n = 500
start = dt.date(2020, 1, 1)
end = start + dt.timedelta(days=n-1)

df_dict = dict(
    time=pd.date_range(start, end),
    value=np.random.randn(n).cumsum()
)

df = pd.DataFrame(df_dict)
g = sns.relplot(x="time", y="value", kind="line", data=df, height=8)

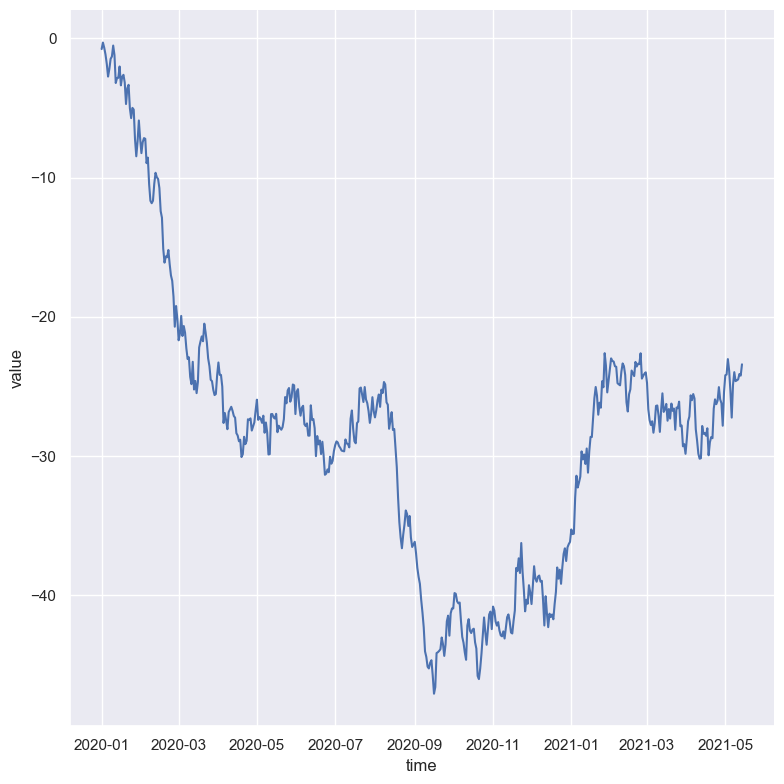
../_images/9f3c52fa6ea4495a6ad0933c29d269f029a29c751141fdab3041f82fcef5a6f8.png

Uwaga!

Ponieważ relplot zakłada, że najczęściej próbujemy narysować y jako funkcję od x, dlatego domyślnym zachowaniem jest sortowanie danych według wartości x narysowaniem wykresu. Sortowanie danych w tym przypadku jest niezwykle istotne - nalezy o tym pamiętać korzystając z innych bibliotek np. matplotlib lub plotly.

# Przypadek gdy wylaczymy sortowanie wzgledem zmiennej "x"
df_dict = dict(
    x=np.random.rand(100),
    y=np.random.rand(100).cumsum()
)

df = pd.DataFrame(df_dict)
g = sns.relplot(x="x", y="y", kind="line", sort = False, data=df, height=8)

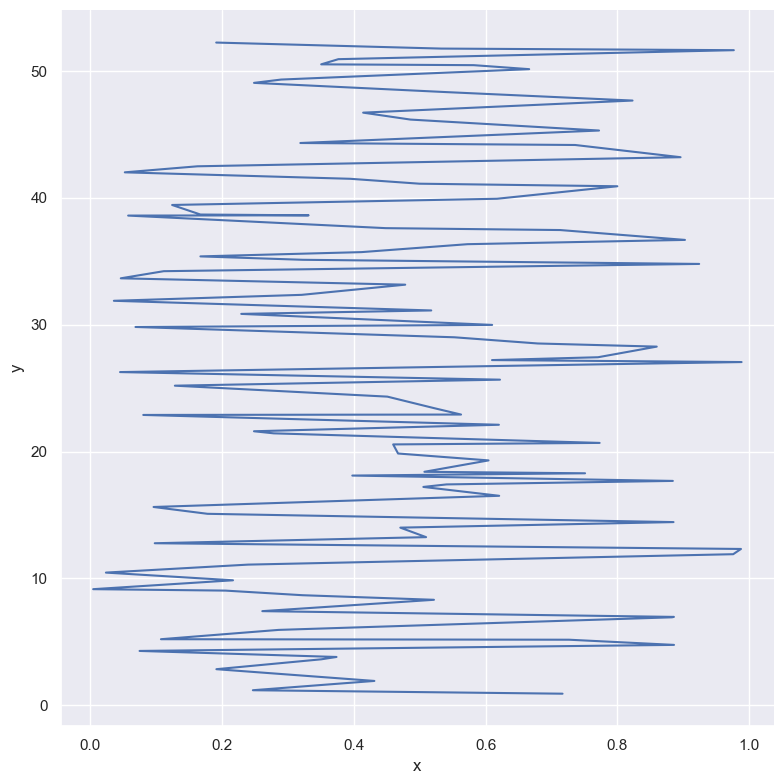
../_images/066b285e49d09384d7c4ecfe1d55ffba6b1a541b1b273eced931d5b8bac961c2.png

Wizualizacja w przypadku agregacji danych#

Bardziej złożone zbiory danych będą miały wiele pomiarów dla tej samej wartości zmiennej x. Domyślnym zachowaniem w seaborn jest agregacja wielokrotnych pomiarów dla każdej wartości x poprzez wykreślenie średniej i 95% przedziału ufności wokół średniej.

sns.relplot(x="timepoint", y="signal", kind="line", data=fmri)

<seaborn.axisgrid.FacetGrid at 0x20b9a85a630>

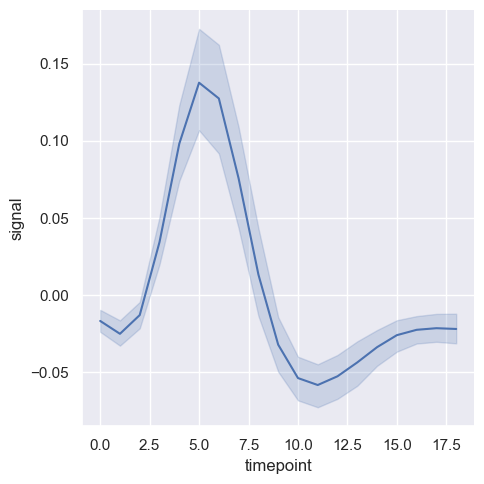
../_images/219f2e2f92dd6aafed03af27e8efcc7762419bb7c27f862d809423af72886635.png

Czasami wykreślenie przedziału ufności może być czasochłonne, dlatego jest możliwość wyłączenia tego wykorzystując parametr errorbar.

sns.relplot(x="timepoint", y="signal", errorbar=None, kind="line", data=fmri)

<seaborn.axisgrid.FacetGrid at 0x20b9a77fb60>

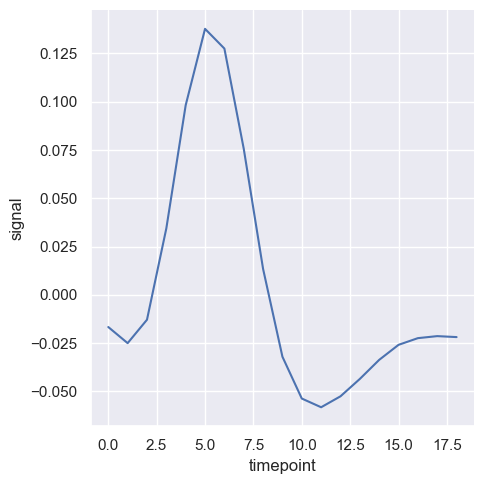
../_images/a4f7043ffa92a7e13f88df716ffb2ecf02487d728b8fcea48db1382f54fe7e47.png

Inną interesującą opcją jest wykreślenie przedziału ufności jako wartość odchylenia standardowego dla danej zmiennej.

sns.relplot(x="timepoint", y="signal", kind="line", errorbar="sd", data=fmri)

<seaborn.axisgrid.FacetGrid at 0x20b9a6c6150>

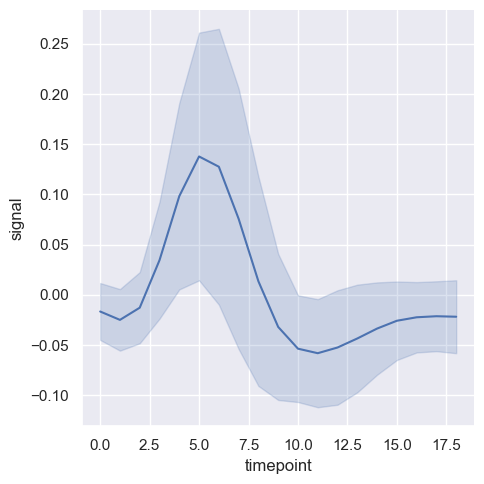
../_images/40310e74bfdba5ce93f632d88a10a88a5281e7b9db0db18dd967e5eb6076a6a8.png

Oczywiście jest możliwość wyłączenia estymacji średniej dla danej zmiennej, jednak w wyniku tej operacji mamy kilka wartości zmiennej y dla zmiennej x. Domyślnym estymatorem jest średnia.

sns.relplot(x="timepoint", y="signal", estimator=None, kind="line", data=fmri)

<seaborn.axisgrid.FacetGrid at 0x20b9c264920>

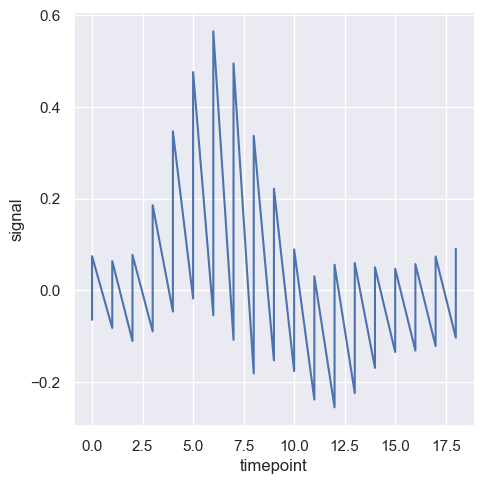
../_images/266f8333d14ce3c053b6dc70434e6a4b7dc56e0a1be6a1ddd323dbc9cd75a86d.png

Funkcja relplot(kind="line") ma taką samą elastyczność co wykres punktowy. Może pokazywać do trzech dodatkowych zmiennych, modyfikując odcień, rozmiar i styl elementów wykresu. Robi to przy użyciu tego samego API.

sns.relplot(x="timepoint", y="signal", hue="event", kind="line", data=fmri)

<seaborn.axisgrid.FacetGrid at 0x20b9c28bbf0>

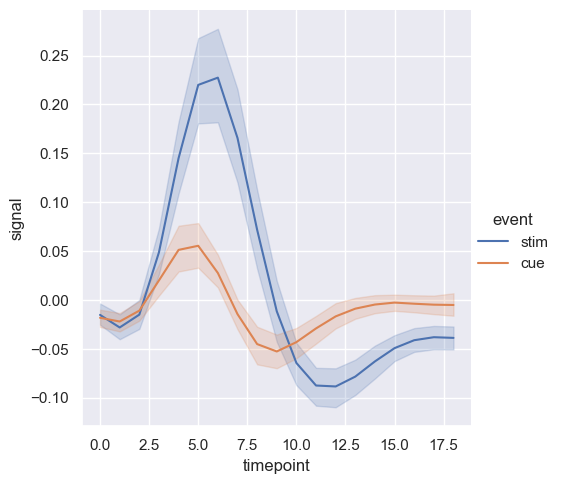
../_images/4a61ebc78650279334e3991d909c176bbd8e1a06c1695774bc01b3bb3e858a4d.png

sns.relplot(x="timepoint", y="signal", hue="region", style="event",
            kind="line", data=fmri)

<seaborn.axisgrid.FacetGrid at 0x20b9c394b30>

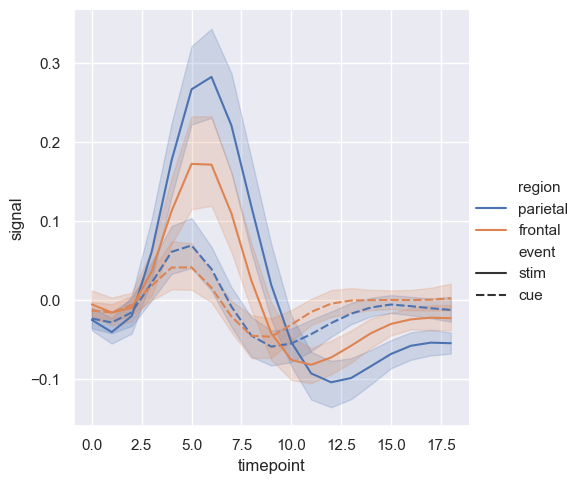
../_images/c12768fddeedc39a80867854239d245e5fda99bdc805fd7351aee642eec7235f.png

sns.relplot(x="timepoint", y="signal", hue="region", style="event",
            dashes=False, markers=True, kind="line", data=fmri);

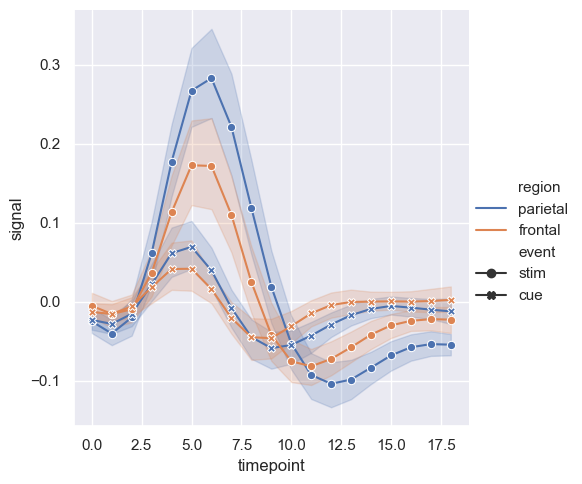
../_images/20e0cbfbda6159cbe7fcbe494f940320afc020f9e672eb926a72c03b72fadc33.png

Taki sam typ wykresu można przedstawić przy pomocy biblioteki matplotlib jednak wtedy wymagana jest większa liczba operacji na danych.

# Data preparation
fmri_agg = fmri.sort_values(by='timepoint').groupby(['timepoint', 'event', 'region']).agg({'signal': 'mean'}).reset_index()

print(f'Wymiar ramki danych: {fmri_agg.shape}')
print(f'Nazwy kolumn: {fmri_agg.columns.values}')

Wymiar ramki danych: (76, 4)
Nazwy kolumn: ['timepoint' 'event' 'region' 'signal']

# Data filters
mask1 = (fmri_agg['event'] == 'cue') & (fmri_agg['region'] == 'frontal')
mask2 = (fmri_agg['event'] == 'cue') & (fmri_agg['region'] == 'parietal')
mask3 = (fmri_agg['event'] == 'stim') & (fmri_agg['region'] == 'frontal')
mask4 = (fmri_agg['event'] == 'stim') & (fmri_agg['region'] == 'parietal')

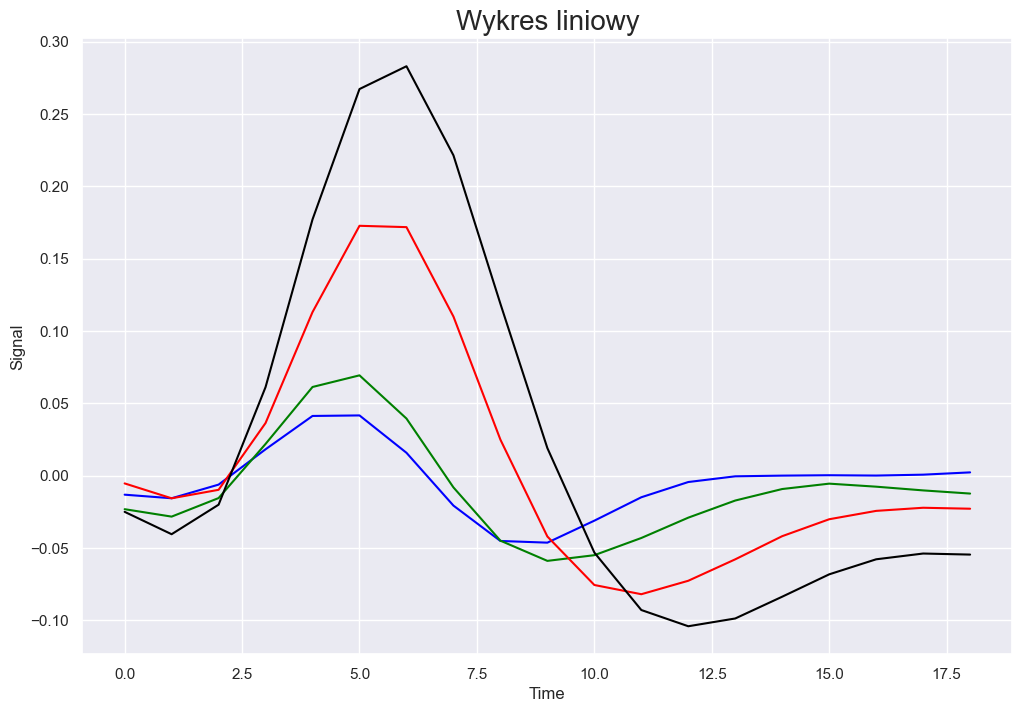
plt.figure(figsize=(12, 8))

plt.plot('timepoint', 'signal', data=fmri_agg[mask1], color='blue')
plt.plot('timepoint', 'signal', data=fmri_agg[mask2], color='green')
plt.plot('timepoint', 'signal', data=fmri_agg[mask3], color='red')
plt.plot('timepoint', 'signal', data=fmri_agg[mask4], color='black')
plt.title('Wykres liniowy', fontsize=20)
plt.xlabel('Time')
plt.ylabel('Signal')

Text(0, 0.5, 'Signal')

../_images/4ded4e595dc572c3c982beb4a67207bd2a4297bd931745a5d4e1b1864d269d4d.png

Wersja z plotly

mask1 = (fmri_agg['event'] == 'cue') & (fmri_agg['region'] == 'frontal')
mask2 = (fmri_agg['event'] == 'cue') & (fmri_agg['region'] == 'parietal')
mask3 = (fmri_agg['event'] == 'stim') & (fmri_agg['region'] == 'frontal')
mask4 = (fmri_agg['event'] == 'stim') & (fmri_agg['region'] == 'parietal')

masks = [mask1, mask2, mask3, mask4]
colors = ['blue', 'green', 'red', 'black']
labels = ['cue / frontal', 'cue / parietal', 'stim / frontal', 'stim / parietal']

fig = go.Figure()

for mask, color, label in zip(masks, colors, labels):
    fig.add_trace(go.Scatter(
        x=fmri_agg.loc[mask, 'timepoint'],
        y=fmri_agg.loc[mask, 'signal'],
        mode='lines+markers',
        line=dict(color=color),
        name=label
    ))

fig.update_layout(
    title="fMRI — mean signal by region and event",
    xaxis_title="Timepoint",
    yaxis_title="Signal",
    legend_title="Event / Region",
    template="plotly_white"
)

fig.show()

Można też dodać przedziały ufności jak w przypadku searborn (trzeba się trochę bardziej napracować)

from scipy import stats

# Compute mean and 95% CI for each group
summary = (
    fmri
    .groupby(["timepoint", "event", "region"])
    .agg(
        mean_signal=('signal', 'mean'),
        sem=('signal', stats.sem),  # standard error
        n=('signal', 'count')
    )
    .reset_index()
)

# Compute 95% confidence interval using t-distribution
summary["ci95"] = stats.t.ppf(0.975, summary["n"] - 1) * summary["sem"]
summary["lower"] = summary["mean_signal"] - summary["ci95"]
summary["upper"] = summary["mean_signal"] + summary["ci95"]

# Define masks
mask1 = (summary['event'] == 'cue') & (summary['region'] == 'frontal')
mask2 = (summary['event'] == 'cue') & (summary['region'] == 'parietal')
mask3 = (summary['event'] == 'stim') & (summary['region'] == 'frontal')
mask4 = (summary['event'] == 'stim') & (summary['region'] == 'parietal')

# Lists for looping
masks = [mask1, mask2, mask3, mask4]
colors = [
    "rgba(0,0,255,1)",     # blue
    "rgba(0,128,0,1)",     # green
    "rgba(255,0,0,1)",     # red
    "rgba(0,0,0,1)"        # black
]
fills = [
    "rgba(0,0,255,0.2)",   # transparent blue
    "rgba(0,128,0,0.2)",   # transparent green
    "rgba(255,0,0,0.2)",   # transparent red
    "rgba(0,0,0,0.2)"      # transparent black
]
labels = ['cue / frontal', 'cue / parietal', 'stim / frontal', 'stim / parietal']

# Create figure
fig = go.Figure()

# Loop through each group
for mask, color, fill, label in zip(masks, colors, fills, labels):
    df = summary.loc[mask].sort_values("timepoint")
    
    # Shaded confidence band
    fig.add_trace(go.Scatter(
        x=pd.concat([df['timepoint'], df['timepoint'][::-1]]),
        y=pd.concat([df['upper'], df['lower'][::-1]]),
        fill='toself',
        fillcolor=fill,
        line=dict(color='rgba(255,255,255,0)'),
        showlegend=False,
        hoverinfo="skip"
    ))
    
    # Mean line
    fig.add_trace(go.Scatter(
        x=df['timepoint'],
        y=df['mean_signal'],
        mode='lines+markers',
        line=dict(color=color),
        name=label
    ))

# Layout
fig.update_layout(
    title="fMRI — mean signal with 95% confidence intervals",
    xaxis_title="Timepoint",
    yaxis_title="Signal",
    legend_title="Event / Region",
    template="plotly_white"
)

fig.show()

Prezentaja wielu relacji na róznych polach wykresu#

Czasami chcemy zrozumieć jakie zachodzą relację między zmiennymi wizualizując je na oddzienlych polach wykresu. W tym przypadku przydatnym staję się parametr col lub row.

sns.relplot(x="timepoint", y="signal", hue="event",
            col="region", kind='line', data=fmri)

<seaborn.axisgrid.FacetGrid at 0x20b9c8daf00>

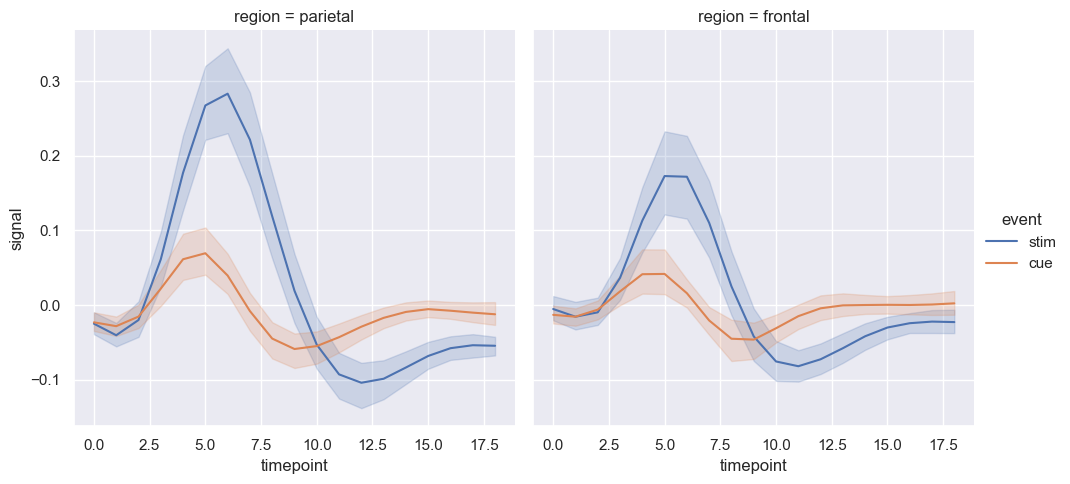
../_images/2f683b59ebc4771cfa768bcceb9dcac6f85b15a521c2d10807fc16444674c2a3.png

W tym przypadku przydatny okazuje się także wykres oparty o plotly. Jego podstawowa forma wygląda następująco:

fig = px.line(data_frame=fmri_agg, x='timepoint', y='signal', color='event', facet_col='region', title='Wykres liniowy')
fig.show()

Czasami do wykresy opartego o seaborn warto dodać parametr col_wrap, który umożliwia nam zdefiniowanie liczby kolumn dla danej wizualizacji.

sns.relplot(x="timepoint", y="signal", hue="event", col="subject", 
            col_wrap=5, kind='line', data=fmri.query("region == 'frontal'"), height=3)

<seaborn.axisgrid.FacetGrid at 0x20b9ca6b350>

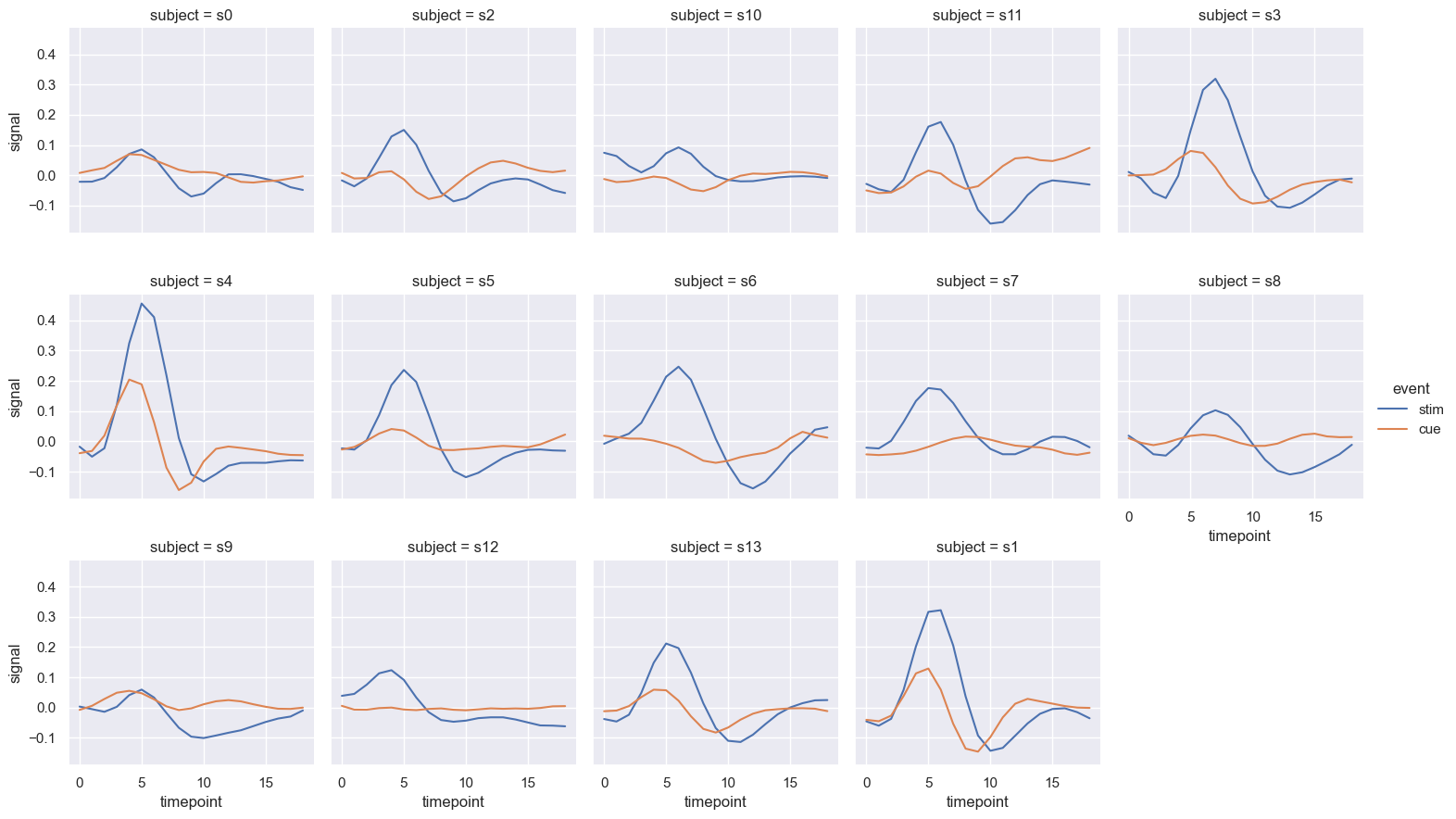
../_images/edc0f9dd8d71bd0ed1a7d4026782f02a93b6fb245f1d2fdbd6e8ffedf8f9213b.png

fmri_frontal = fmri.query("region == 'frontal'").sort_values(["subject", "event", "timepoint"])

fig = px.line(
    fmri_frontal,
    x="timepoint",
    y="signal",
    color="event",
    facet_col="subject",
    facet_col_wrap=5,
    height=700
)

fig.update_layout(
    template="plotly_white",
    showlegend=True
)

fig.show()

Wizualizacja rozkładu zmiennych#

Jednym z pierwszych kroków podczas budowy modeli uczenia maszynowego powinno być zrozumienie, w jaki sposób rozkładają się zmienne. Techniki wizualizacji rozkładu zmiennych mogą dostarczyć szybkich odpowiedzi na wiele ważnych pytań. Jaki zakres obejmują obserwacje? Jaka jest ich główna tendencja? Czy są mocno przekrzywione w jednym kierunku? Czy istnieją znaczące wartości odstające? Czy odpowiedzi na te pytania różnią się w podzbiorach zdefiniowanych przez inne zmienne?

Biblioteka seaborn zawiera kilka bardzo przydatnych funkcji pod kątem badania rozkładu tj. histplot(), kdeplot(), ecdfplot() i rugplot(). Są one zgrupowane w ramach funkcji displot(), jointplot() i pairplot().

Istnieje kilka różnych podejść do wizualizacji rozładu zmiennych, a każde z nich ma swoje względne zalety i wady. Ważne jest, aby zrozumieć te czynniki, aby wybrać najlepsze podejście do konkretnego celu.

Rozkład zmiennej jednowymiarowej#

Najczęstszym podejściem do wizualizacji rozkładu jest histogram, który jest graficzną reprezentacją danych, która agreguje grupę punktów w zakresy określone przez analityka. Podobnie jak w przypadku wykresu słupkowego, histogram kondensuje obserwacje w łatwo interpretowalną wizualizację. Histogram jest jedną z podstawowych form wizualizacji wykorzystywaną w celu określenie rozkładu danej cechy. Podczas pracy z danymi często kluczowym jest aby określić w jaki sposób rozkładają się nasze dane - takie informacje można wtedy wykorzystać w dalszej pracy m.in. określając rodzaj algorytmu czy dokonując różnego rodzaju transformacji danej zmiennej.

sns.displot(housing, x="MedHouseVal")

<seaborn.axisgrid.FacetGrid at 0x20b9ac078c0>

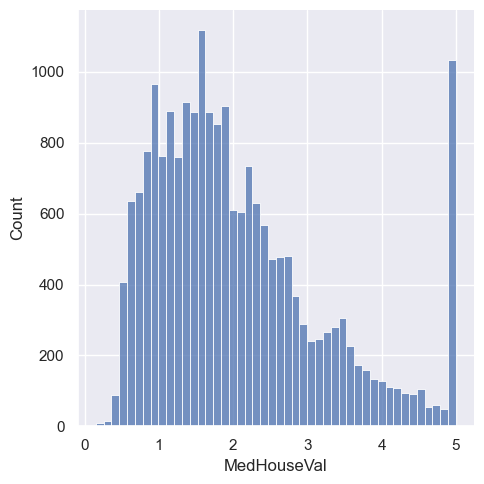
../_images/e5b7af975520b10f03252a12506f598441a6eeec52dc909ee28a4fadbfdbe8b0.png

Powyższy histogram dla zmiennej MedHouseVal w bardzo szybki sposób jest w stanie przedstawić nam pewne kluczowe informacje na temat zmiennej celu. Przykładem może być kwestia najpopularniszych wartości tej zmiennej która jest na poziomie około 1.5 oraz 5. Jednak bardzo ciekawą sytuacją jest kwestia wartości 5, która jest bardzo popularna jednak z drugiej strony może być pewnego rodzaju błędem - zwłaczsza jak spojrzymy na rozkład zmiennej bez wartości 5, gdzie wartości dla tego ogona są malejące.

W przypadku histogramu bardzo ważną rolę odgrywają parametry bins lub binwdith, które mówią nam o wielkości lub długości przedziałów dla histogramu. Te same dane przedstawione z inną wartością parametru binwidth mogą nam odpowiedzieć na zadane pytanie w zupełnie inny sposób. Przykładam jesy poniższy histogram na którym nie widać żadnych anomalii dla wartości zmiennej równej 5.

sns.displot(housing, x="MedHouseVal", binwidth=1)

<seaborn.axisgrid.FacetGrid at 0x20b9aa18800>

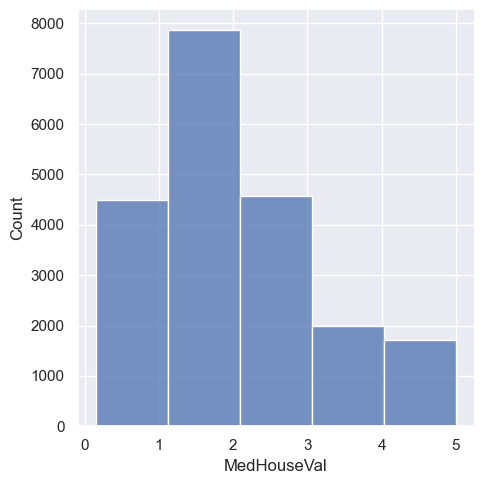
../_images/f8b87eb2c7b72cd5e038dc2fc379a9774c6895729823b7aefa87fb08d19bf916.png

Dodatkowo pokażmy jak ten sam wykres wyglądałby z wykorzystaniem pakietów matplotlib oraz plotly - oczywiście poniższe wizualizacje uwzględniają domyślne opcje.

plt.figure(figsize=(8, 6))
plt.hist(x='MedHouseVal', data=housing, bins=5)
plt.title('Histogram', fontsize=20)
plt.ylabel('Frequency')
plt.xlabel('MedHouseVal')        

Text(0.5, 0, 'MedHouseVal')

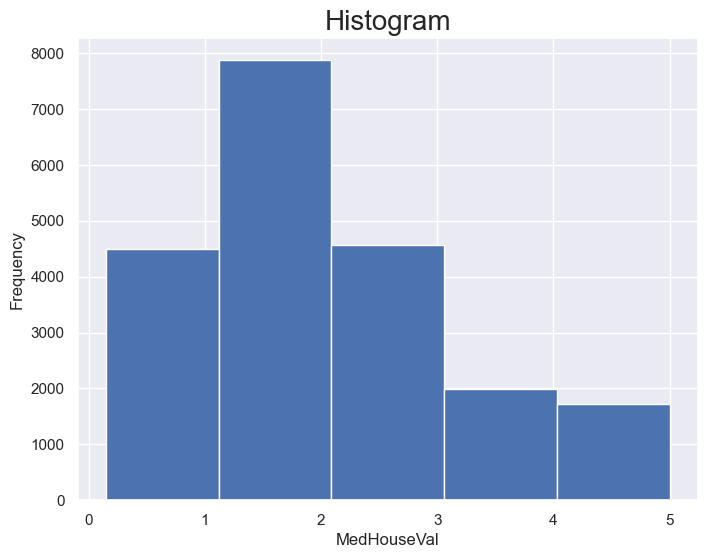
../_images/d2de21bacf4518008d1e726dd5d138ce42f31a4df08c6f2598733599c95208d8.png

fig = px.histogram(data_frame=housing, x='MedHouseVal', nbins=5, title='Histogram')
fig.update_layout(bargap=0.2)
fig.show()

Wizualizacja zmiennych kategorycznych#

Możliwa jest również wizualizacja rozkładu zmiennej kategorycznej za pomocą logiki histogramu. W tym przypadku pomocny może być parametr shrink, który nieco zwężą słupki aby podkreślić kategorialny charakter osi.

sns.displot(housing, x="MedInc_greater_5", shrink=0.7)

<seaborn.axisgrid.FacetGrid at 0x20b9aca8e60>

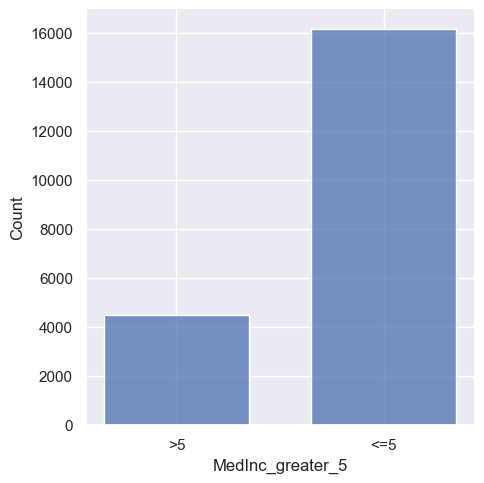
../_images/f04a35aaf9f434e0f52b64c45e3a982dcd1439506d6eeab0e88ce13f4d687b2d.png

Rozkład warunkowy względem innych zmiennych#

Po zrozumieniu rozkładu zmiennej, następnym krokiem jest często pytanie, czy cechy tego rozkładu różnią się od innych zmiennych w zbiorze danych. displot zapewnia obsługę podzbiorów warunkowych poprzez barwy.

sns.displot(fmri, x='signal', hue="region")

<seaborn.axisgrid.FacetGrid at 0x20b9e9af6e0>

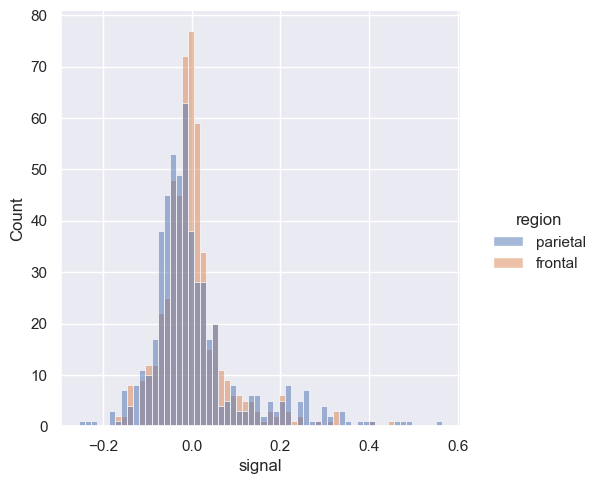
../_images/3c7c0e32ca2afd5efd15344868e82369f367fd26638842a9c3419abd9fd71a54.png

Czasam warto nieco zmienić wizualizacje naszych danych poprzez zmianę wartości parametru element na step. Pomaga to czasem nieco lepiej zauwazyć różnicę w danych.

sns.displot(fmri, x='signal', hue="region", element='step')

<seaborn.axisgrid.FacetGrid at 0x20b9ac07bf0>

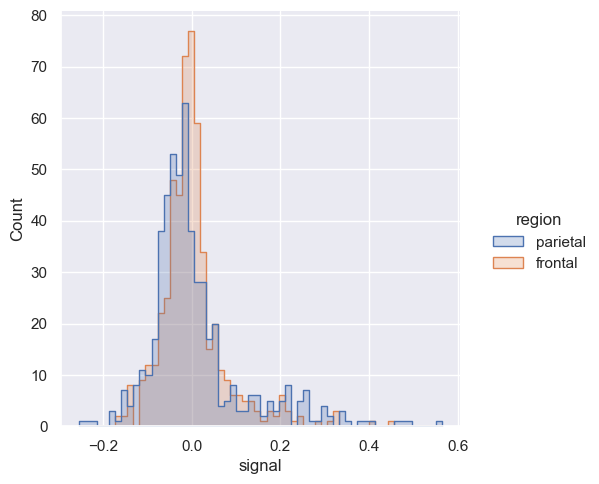
../_images/6e33ccaeb37642ca1887e1123e67ccc29006935d7119e7064bf2fbf83ab68ad0.png

Innym rozwiązaniem jest pokazanie rozkładów, które się na siebie nakładają.

sns.displot(fmri, x='signal', hue="region", multiple='stack')

<seaborn.axisgrid.FacetGrid at 0x20b9eaf95b0>

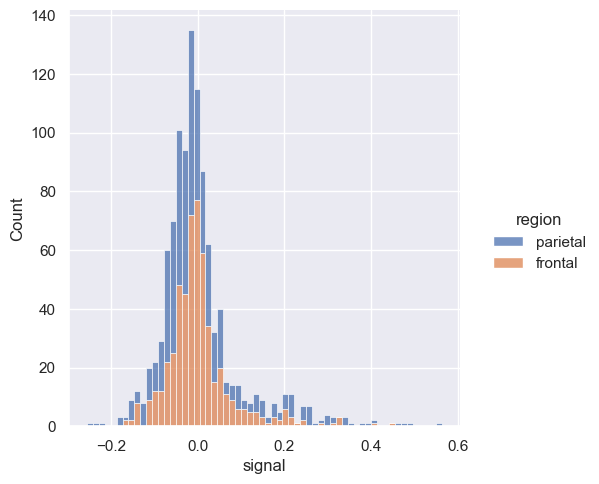
../_images/30cc9a5a1834570e314afd63778c49f3d96662dbd89f4b05a19b4b20ff0d4bb4.png

sns.displot(fmri, x='signal', hue="region", multiple='dodge')

<seaborn.axisgrid.FacetGrid at 0x20b9ea80a70>

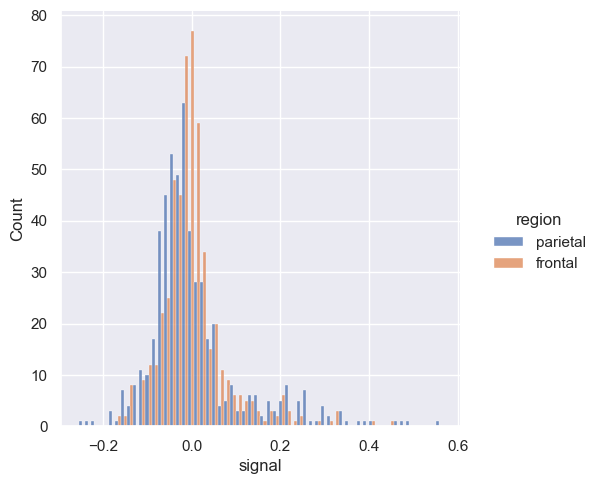
../_images/195ecac02a0069574ff9d33215a70936d3f376443be8469cebe5c150d9dda715.png

Rozkłady możemy też pokazać na dwóch osobnych wykresach.

sns.displot(fmri, x='signal', col="region")

<seaborn.axisgrid.FacetGrid at 0x20ba07fe870>

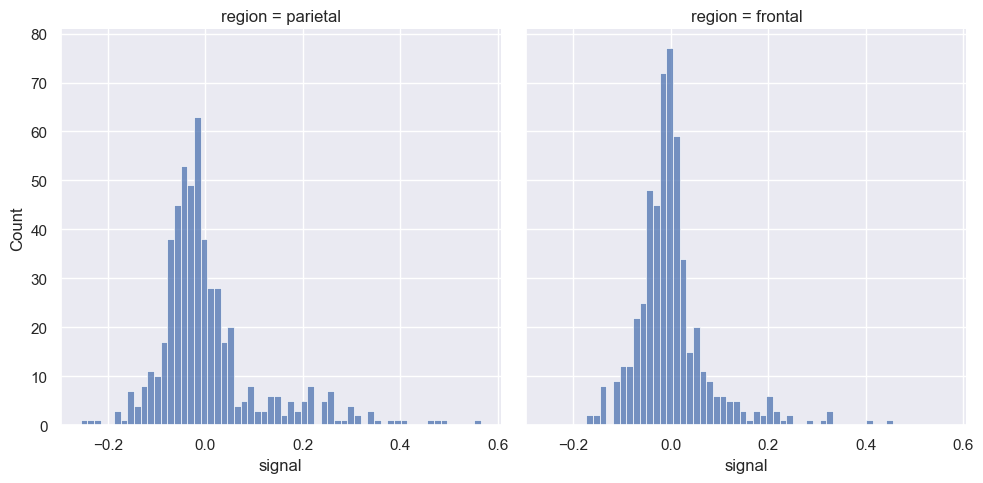
../_images/e2bd4be620f50cd64c5b8d7f6622749b6e7974af35ae1e030697b44143bd3074.png

Wnioski

Wybór wizualizacji zależy głównie od analityka i od problemu, który chciałby rozwiązać. Róznego rodzaju dane wymagają róznego podejścia.

Wartym zaznaczenia jest jeszcze jeden przydatny parametr, mianowicie stat. Umożliwia on nam zmianę sposobu wyświetlenia zmiennej z domyślnej count na density lub probability.

sns.displot(fmri, x='signal', hue="region", stat='density')

<seaborn.axisgrid.FacetGrid at 0x20b9ab78e00>

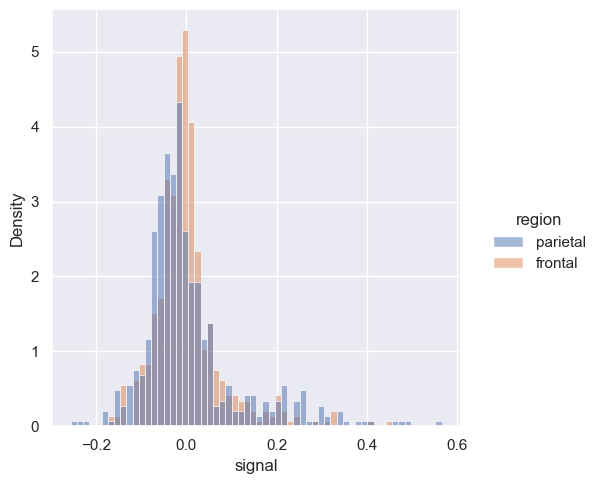
../_images/8a0cb60a9542bb520ae6f84769ceb9b88a5dcf92c0a46671e4aa8463c3d68c07.png

sns.displot(fmri, x='signal', hue="region", stat='probability')

<seaborn.axisgrid.FacetGrid at 0x20b9eafb140>

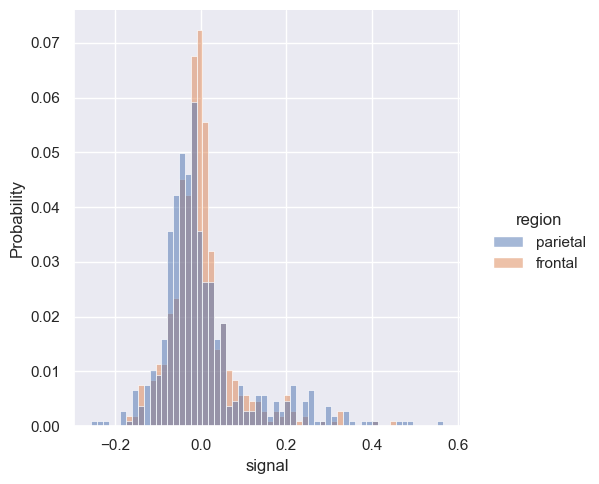
../_images/b2700d5d3a141471fa19b8c4c3a1bcbec46475a150354a6ce656abc1ce985f1a.png

To samo w plotly

fig = px.histogram(fmri, x='signal', color="region", opacity=0.6)
fig.update_layout(bargap=0.2, barmode='overlay')
fig.show()

fig = px.histogram(fmri, x='signal', color="region")
fig.update_layout(bargap=0.2, barmode='stack')
fig.show()

Warto zauważyć, że w przypadku poniższych wykresów została zmieniona skala ze zliczania na procent.

x0 = fmri.loc[fmri['region'] == 'frontal', 'signal']
x1 = fmri.loc[fmri['region'] == 'parietal', 'signal']

fig = go.Figure()
fig.add_trace(go.Histogram(
    x=x0,
    histnorm='percent',
    name='frontal',
    marker_color='#EB89B5',
    opacity=0.75
))
fig.add_trace(go.Histogram(
    x=x1,
    histnorm='percent',
    name='temporal',
    marker_color='#330C73',
    opacity=0.75
))

fig.update_layout(
    title_text='Signal grouped by region',
    xaxis_title_text='Signal',
    yaxis_title_text='Percent',
    bargap=0.2,
    bargroupgap=0.1
)

fig.show()

from plotly.subplots import make_subplots

x0 = fmri.loc[fmri['region'] == 'frontal', 'signal']
x1 = fmri.loc[fmri['region'] == 'parietal', 'signal']

fig = make_subplots(rows=1, cols=2)

trace0 = go.Histogram(
    x=x0,
    histnorm='percent',
    name='frontal',
    marker_color='#EB89B5',
    opacity=0.75
)
trace1 = go.Histogram(
    x=x1,
    histnorm='percent',
    name='temporal',
    marker_color='#330C73',
    opacity=0.75
)
fig.add_trace(trace0, 1, 1)
fig.add_trace(trace1, 1, 2)

fig.update_layout(
    title_text='Signal grouped by region',
    xaxis_title_text='Signal',
    yaxis_title_text='Percent',
    bargap=0.2,
    bargroupgap=0.1
)

fig.show()

Gęstość rozkładu#

Histogram ma na celu przybliżenie podstawowej funkcji gęstości prawdopodobieństwa, która wygenerowała dane, poprzez grupowanie i liczenie obserwacji. Szacowanie gęstości jądra (KDE) przedstawia inne rozwiązanie tego samego problemu. Zamiast używać oddzielnych przedziałów, wykres KDE wygładza obserwacje za pomocą jądra Gaussa, tworząc ciągłe oszacowanie gęstości rozkładu.

sns.displot(fmri, x='signal', kind='kde')

<seaborn.axisgrid.FacetGrid at 0x20ba1382c90>

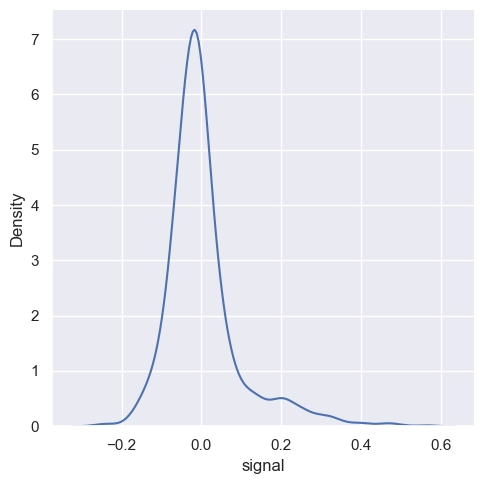
../_images/f330888eb7b6b348027077de09b8de11481683fb772e9ab056263298201cf3e9.png

Podobnie jak w przypadku histogramu, wykres kde posiada parametr bw_adjust (parametr wygładzenia), który spełnia podobną rolę co binwidth lub bins dla histogramu. Ustawnienie tego parametru na zbyt niskim poziomie spowoduje nadmierne dopasowanie dodanych, w odwrotnym przypadku nadrmierne wygładzenie spowoduję wymazanie znaczących cech rozkładu.

sns.displot(fmri, x='signal', kind='kde', bw_adjust=0.1)

<seaborn.axisgrid.FacetGrid at 0x20ba1592750>

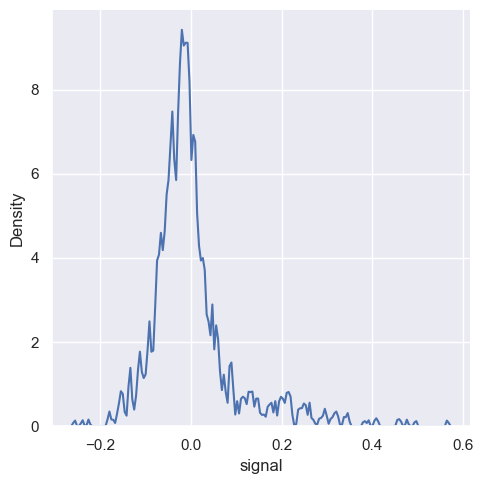
../_images/ce70e6e8336c21ca3f44ed784f61e5ef0c315c2780518735ce1f41eb1db027c0.png

sns.displot(fmri, x='signal', kind='kde', bw_adjust=2)

<seaborn.axisgrid.FacetGrid at 0x20ba15a4140>

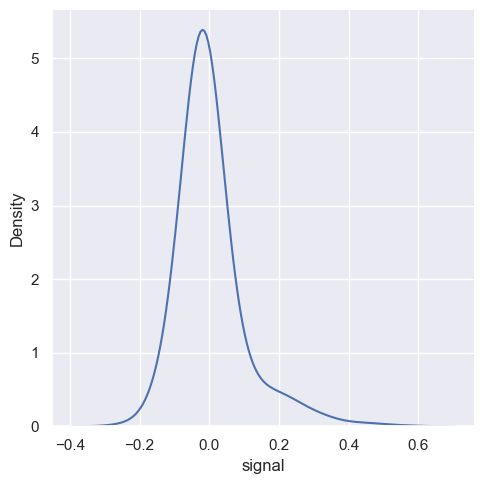
../_images/00a85d0faed6e531f2b666148df951babc4997ae0d14bf151fc04d3ae9608c92.png

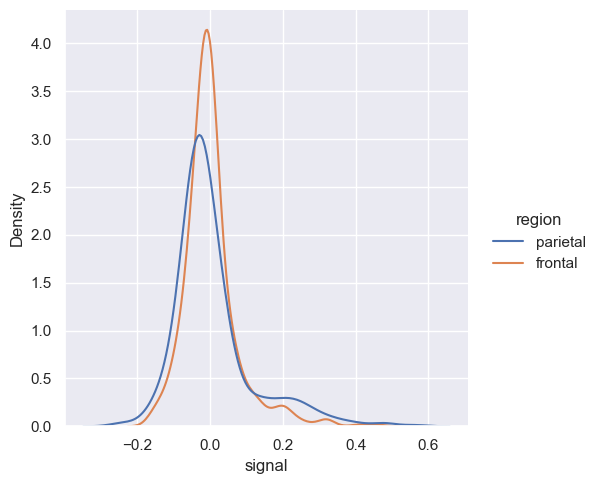
Rozkład gęstości ma podobne funkcjonalności jak wyżej przedstawiony histogram. Oto kilka z nich:

sns.displot(fmri, x="signal", hue="region", kind="kde")

<seaborn.axisgrid.FacetGrid at 0x20ba1591b20>

../_images/8a1970b00863eb54b65065e760ba9c21bb5240e8f0b24ba04c31f8fb331584e5.png

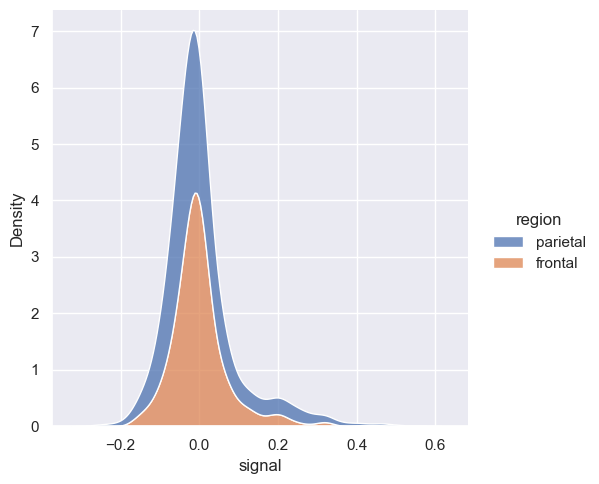
sns.displot(fmri, x="signal", hue="region", multiple='stack', kind="kde")

<seaborn.axisgrid.FacetGrid at 0x20ba15eb440>

../_images/5e5ca702466a05c3323c434f6b5fb1936ad85fe79437fa5373953b9268917090.png

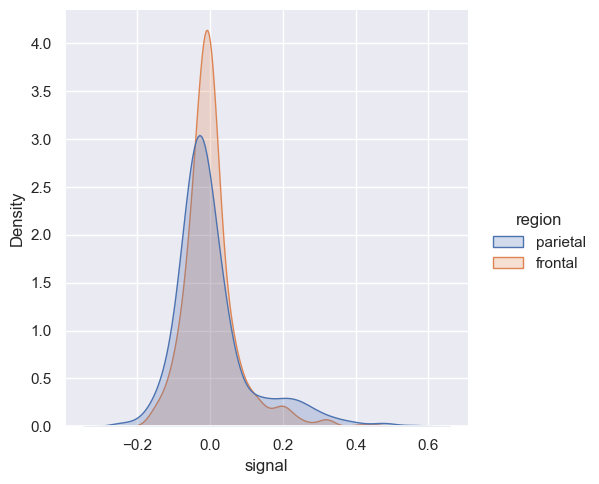
sns.displot(fmri, x="signal", hue="region", fill=True, kind="kde")

<seaborn.axisgrid.FacetGrid at 0x20ba15a5b20>

../_images/559d6a94aeec194a7870de8b0eb25c2263659cbec68ac182f01ee9df94c5c33d.png

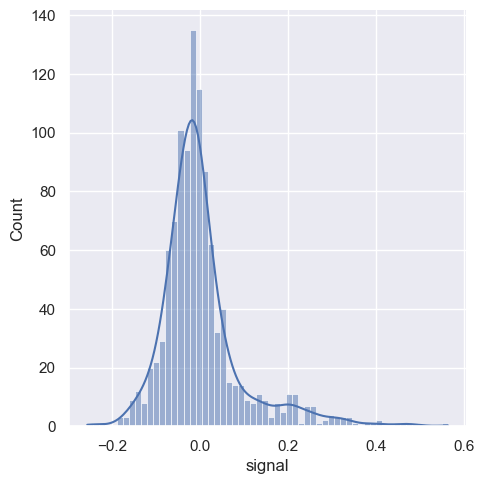
Bardzo częstym podejściem podczas wizualizacji danych jest skorzystanie z obu typów wykresu jednocześnie.

sns.displot(fmri, x="signal", kde=True)

<seaborn.axisgrid.FacetGrid at 0x20ba5259040>

../_images/83d6d578ddfcab31c296c51b25b8327a30a68c7d8bec119c31ff89246c59332d.png

import plotly.figure_factory as ff

x0 = fmri.loc[fmri['region'] == 'frontal', 'signal']
x1 = fmri.loc[fmri['region'] == 'parietal', 'signal']

hist_data = [x0, x1]

group_labels = ['Frontal', 'Parietal']
colors = ['#A56CC1', '#63F5EF']

# Create distplot with curve_type set to 'normal'
fig = ff.create_distplot(hist_data, group_labels, colors=colors,
                         bin_size=.01, show_rug=False)

# Add title
fig.update_layout(title_text='Histogram with KDE', bargap=0.05)
fig.show()

Dystrybuanta rozkładu#

Trzecia opcja wizualizacji rozkładów oblicza empiryczną dystrybuantę rozkładu (ECDF).

sns.displot(fmri, x="signal", kind='ecdf')

<seaborn.axisgrid.FacetGrid at 0x20ba6505c70>

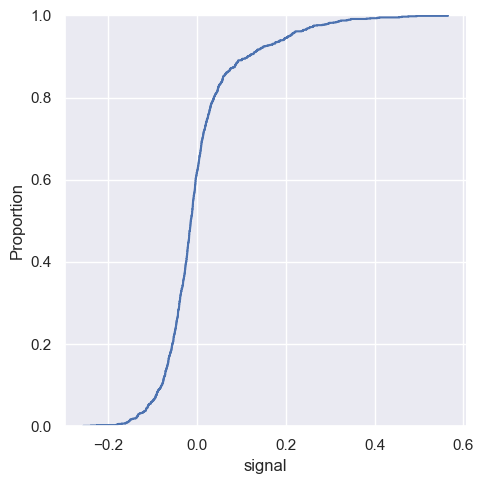
../_images/550fabbf29bef350c6d75197b41e562490abeb9c40d6a99c0f43b813e6d7476c.png

Wizualizacja dystrybuanty rozkładu ma dwie istotne zalety. Po pierwsze bezpośrednio reprezentuje każdy punkt danych. Oznacza to, że nie trzeba brać pod uwagę rozmiaru przedziału ani parametru wygładzania. Dodatkowo, ponieważ krzywa rośnie monotonicznie, dobrze nadaje się do porównywania wielu rozkładów.

sns.displot(fmri, x="signal", hue="region", kind="ecdf")

<seaborn.axisgrid.FacetGrid at 0x20ba522cb30>

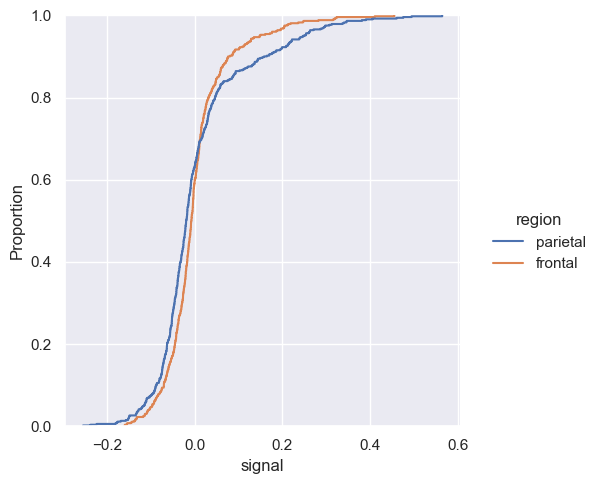
../_images/98a31191a3f645a70e20283a250dfc9b9a47a7153a8c4985af83094397b100d8.png

Główną wadą wykresu dystrybuanty jest to, że mniej intuicyjnie przedstawia kształt rozkładu niż histogram lub krzywa gęstości.

fig = px.ecdf(fmri, x="signal", color="region")
fig.show()

Rozkład wielowymiarowy#

Wszystkie dotychczasowe przykłady uwzględniały rozkłady jednowymiarowe: rozkłady jednej zmiennej, z uwzględnieniem zależności od drugiej zmiennej przypisanej do barwy. Teraz zajemiemy się badaniem rozkładów dwuwymiarowych.

sns.displot(housing, x="MedHouseVal", y="MedInc")

<seaborn.axisgrid.FacetGrid at 0x20ba52e3620>

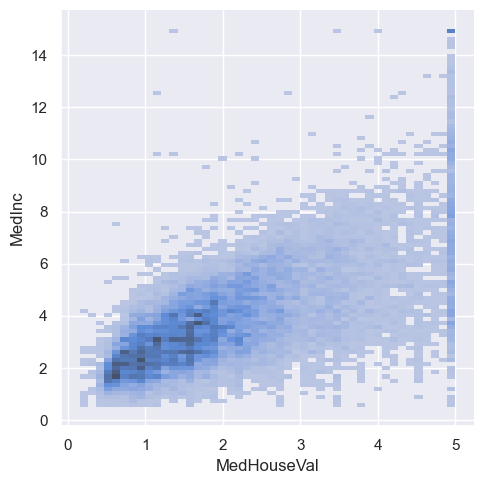
../_images/181ef042e3124b471e582b9ccff8373cc44f8e2e689d6312459cbc47687b0247.png

fig = px.density_heatmap(
    housing,
    x="MedHouseVal",
    y="MedInc",
    nbinsx=30,
    nbinsy=30,
    color_continuous_scale="Viridis"
)

fig.update_layout(
    template="plotly_white",
    title="2D Distribution of Median House Value vs Median Income"
)

fig.show()

sns.displot(housing, x="MedHouseVal", y="MedInc", kind='kde')

<seaborn.axisgrid.FacetGrid at 0x20ba5367bf0>

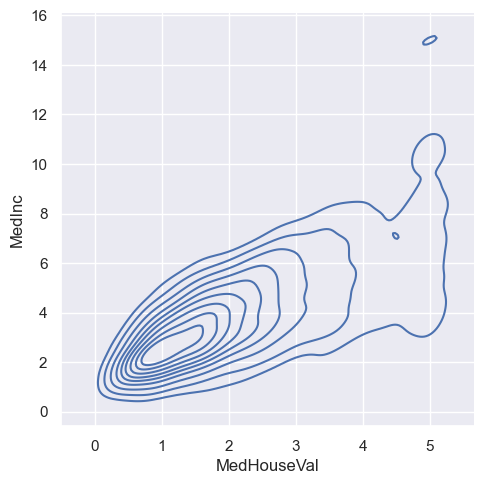
../_images/603fb0374bdc6be9840e80fbd352c79271cda0e4f504dda766bfd60979b397f7.png

fig = px.density_contour(
    housing,
    x="MedHouseVal",
    y="MedInc"
    )
fig.update_traces(contours_coloring="fill", contours_showlabels=True)
fig.update_layout(
    template="plotly_white",
    title="2D Density Contour of Median House Value vs Median Income"
)
fig.show()

sns.displot(housing, x="MedInc", y="MedHouseVal", hue="AveRooms_greater_5")

<seaborn.axisgrid.FacetGrid at 0x20ba6a3f2f0>

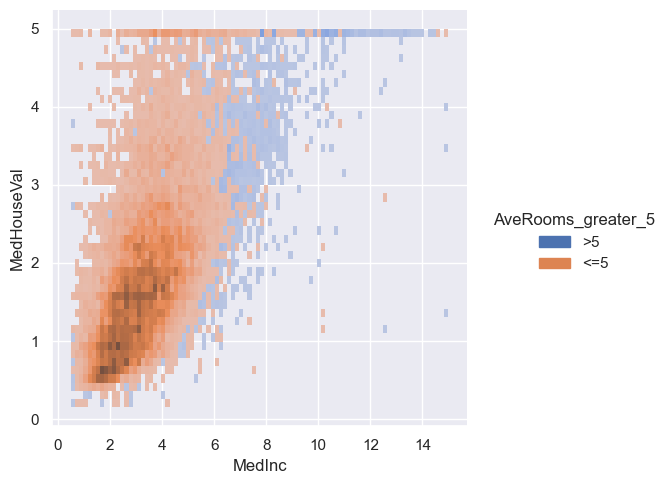
../_images/b8b3824e6a1d7f888bb1b12f957b2ec397409bd39a33a484c520e64617688607.png

fig = px.density_heatmap(
    housing,
    x="MedInc",
    y="MedHouseVal",
    nbinsx=30,
    nbinsy=30,
    facet_col="AveRooms_greater_5",
    color_continuous_scale="Viridis"
)

fig.update_layout(
    template="plotly_white",
    title="2D Distribution by AveRooms_greater_5"
)

fig.show()

sns.displot(housing, x="MedInc", y="MedHouseVal", hue="AveRooms_greater_5", kind='kde')

<seaborn.axisgrid.FacetGrid at 0x20ba80230b0>

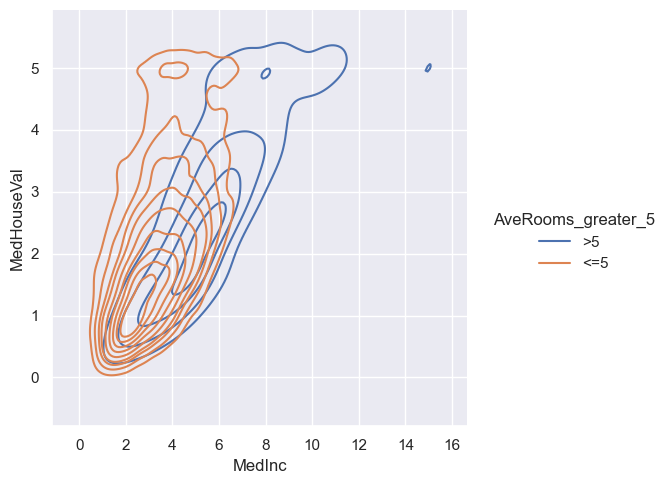
../_images/8e0ebbe32bc2e1ed3e1da3f69edb6cb5b4dfe4c1c98e4c9f65c2f49c51662169.png

colorscales = {
    '<=5': "Blues",
    '>5': "Reds"
}

fig = go.Figure()

for group, df in housing.groupby("AveRooms_greater_5"):
    fig.add_trace(
        go.Histogram2dContour(
            x=df["MedInc"],
            y=df["MedHouseVal"],
            colorscale=colorscales[group],
            contours=dict(coloring="fill"),
            opacity=0.6,
            name=f"AveRooms > 5: {group}",
            showlegend=True,
            showscale=False
        )
    )

fig.update_layout(
    template="plotly_white",
    title="2D Density Contours of MedHouseVal vs MedInc by AveRooms_greater_5",
    xaxis_title="Median Income",
    yaxis_title="Median House Value"
)

fig.show()

Jak widać każdy z powyższych wykresów posiada podobne lub wręcz takie same parametry jak w przypadku wykresów jednowymiarowych. Zachęcam do zgłębienia innych dodatkowych opcji pod kątem analizy rozkładu jedno i dwuwymiarowego.

Ostatnim typem wykresu, który warto mieć w zanadrzu podczas analizy rozkładu jest jointplot.

sns.jointplot(data=housing, x="MedInc", y="MedHouseVal")

<seaborn.axisgrid.JointGrid at 0x20ba804d7f0>

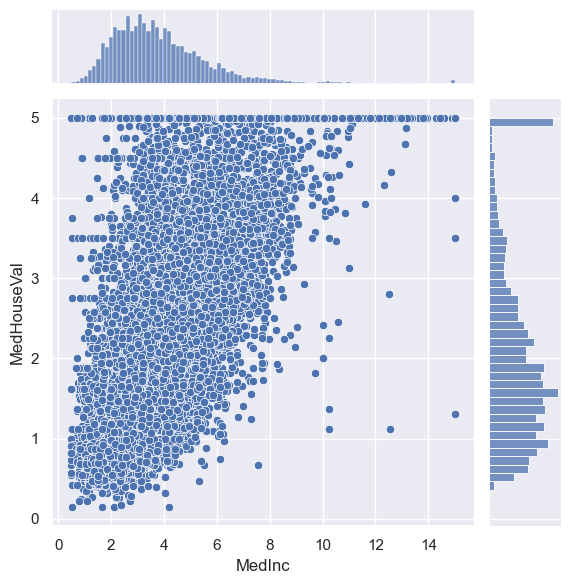
../_images/45dad9b45c40e685d2758d226fae3c404557346abaa5cdadbd5c4e38f979518b.png

fig = px.scatter(
    housing,
    x="MedInc",
    y="MedHouseVal",
    marginal_x="histogram",
    marginal_y="histogram",
    opacity=0.6,
    template="plotly_white",
    title="Joint Distribution of Median Income and Median House Value"
)

fig.show()

sns.jointplot(data=housing, x="MedInc", y="MedHouseVal", hue="AveRooms_greater_5", kind='kde')

<seaborn.axisgrid.JointGrid at 0x20ba6e48140>

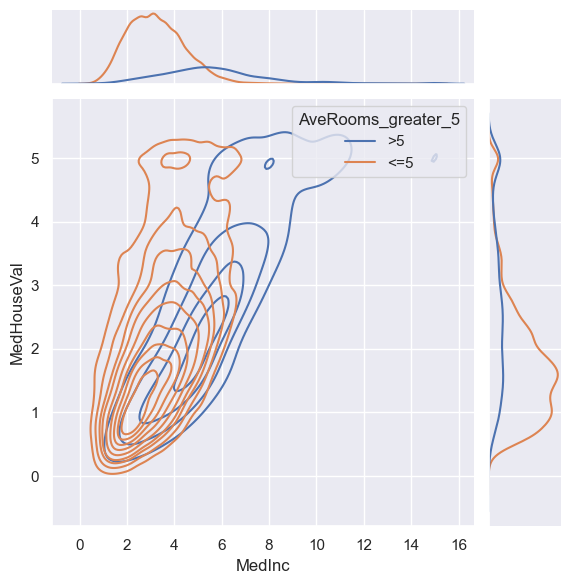
../_images/a40171955457682b845b30e9923e43e1465a0f1df26f15516d4462cedf1c8633.png

W pltoly nie można tak łatwo rozrysować typu kde dla pojedynczych kolumn.

Możliwe typu wykresów: histogram, rug, box, violin.

fig = px.density_contour(
    housing,
    x="MedInc",
    y="MedHouseVal",
    color="AveRooms_greater_5",
    marginal_x="violin",
    marginal_y="violin",
    template="plotly_white",
    title="2D KDE of Median Income vs House Value by AveRooms_greater_5"
)

fig.update_traces(opacity=0.6)

fig.show()

Zaletą wykresy typu joinplot jest dodatkowe wyświetlanie jednowymiarowego rozkładu zmiennej w postaci histogramu lub funkcji gęstości. Dzięki temu możemu jeszcze lepiej zrozumieć relacje zachodzące w naszym zbiorze danych.

Wizualizacja modeli regresyjnych#

Zazwyczaj zbiory danych zawierają wiele zmiennych numerycznych, a celem analizy jest często powiązanie tych zmiennych ze sobą. Wcześniej omówione funkcje pokazują łączny rozkład dwóch zmiennych lub pewne ich relacje określone wykresem punktowym. Bardzo pomocne może być jednak wykorzystanie modeli statystycznych do oszacowania prostej zależności między dwoma zaszumionymi zestawami obserwacji.

Info

Pakiet seaborn nie jest pakietem do analizy statystycznej. Aby uzyskać miary ilościowe związane z dokładnym dopasowaniem modeli regresji, należy użyć modeli statystycznych zawartych w bibliotekach sklearn czy statsmodels.

Wizualizacja regresji liniowej#

W seaborn wykorzystywane są dwie główne funkcje do wizualizacji zależności liniowej określonej za pomocą regresji. Te funkcje to: regplot() i lmplot(). Obie funkcje są ze sobą ściśle powiązane i dzielą większość swoich podstawowych parametrów.

W najprostszym użyciu obie funkcje rysują wykres rozrzutu dwóch zmiennych, x i y, a następnie dopasowują model regresji y ~ x. Następnie wykreślają wynikową linię regresji oraz 95% przedział ufności.

sns.regplot(x="total_bill", y="tip", data=tips)

<Axes: xlabel='total_bill', ylabel='tip'>

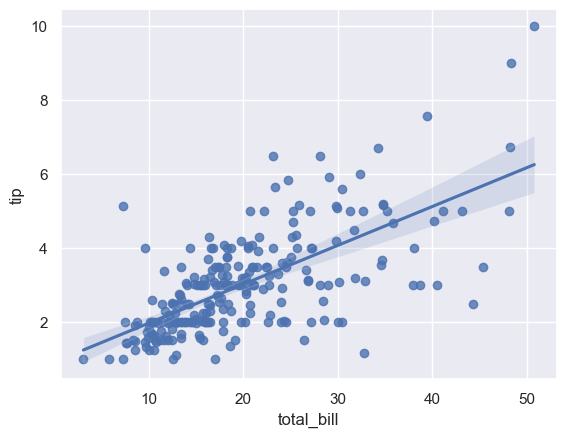
../_images/79f7e0a5a9b542ee0deab9629bd6f63978561038e03487abda0852db69674398.png

fig = px.scatter(
    tips,
    x="total_bill",
    y="tip",
    trendline="ols",
    template="plotly_white",
    title="Tip vs Total Bill with Linear Regression Line"
)

fig.show()

results = px.get_trendline_results(fig)
ols_result = results.iloc[0]["px_fit_results"]
print(ols_result.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.457
Model:                            OLS   Adj. R-squared:                  0.454
Method:                 Least Squares   F-statistic:                     203.4
Date:                Mon, 12 Jan 2026   Prob (F-statistic):           6.69e-34
Time:                        00:55:38   Log-Likelihood:                -350.54
No. Observations:                 244   AIC:                             705.1
Df Residuals:                     242   BIC:                             712.1
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.9203      0.160      5.761      0.000       0.606       1.235
x1             0.1050      0.007     14.260      0.000       0.091       0.120
==============================================================================
Omnibus:                       20.185   Durbin-Watson:                   1.811
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               37.750
Skew:                           0.443   Prob(JB):                     6.35e-09
Kurtosis:                       4.711   Cond. No.                         53.0
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

sns.lmplot(x="total_bill", y="tip", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bae207bf0>

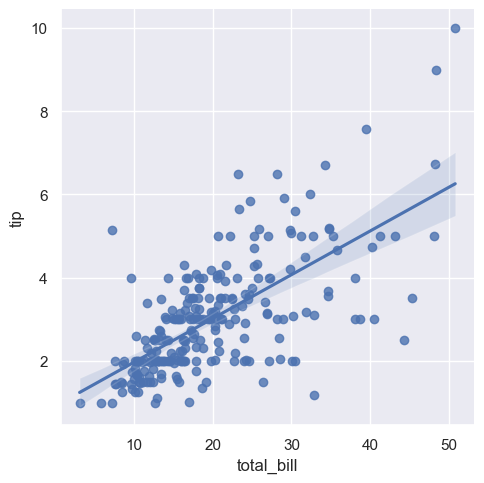
../_images/3376ab5038c5abab2dd18108d930006936c3ed82a00e958916b8a500b9646f32.png

W poniższym notatniku w głównej mierze skupimy się na funkcji lmplot.

Możliwe jest dopasowanie regresji liniowej, gdy jedna ze zmiennych przyjmuje wartości dyskretne, jednak prosty wykres rozrzutu utworzony przez ten rodzaj danych często jest nieoptymalny.

sns.lmplot(x="size", y="tip", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bae28a690>

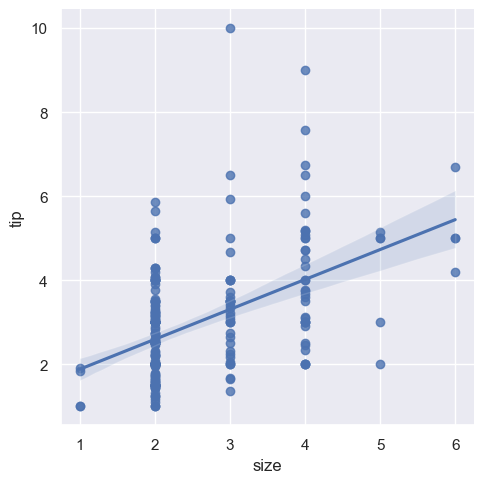
../_images/c4d72c11f5b2d288ba49de4eb6ee1f4d1fedd09081edd36779daa16d2cd32712.png

fig = px.scatter(
    tips,
    x="size",
    y="tip",
    trendline="ols",            # Ordinary Least Squares regression line
    template="plotly_white",
    title="Linear Regression of Tip vs Table Size"
)

fig.show()

Jedną z opcji rozwiązania tego problemu jest dodanie losowego szumu jitter do wartości dyskretnych, aby rozkład tych wartości był bardziej przejrzysty.

sns.lmplot(x="size", y="tip", data=tips, x_jitter=.05)

<seaborn.axisgrid.FacetGrid at 0x20bae29bb30>

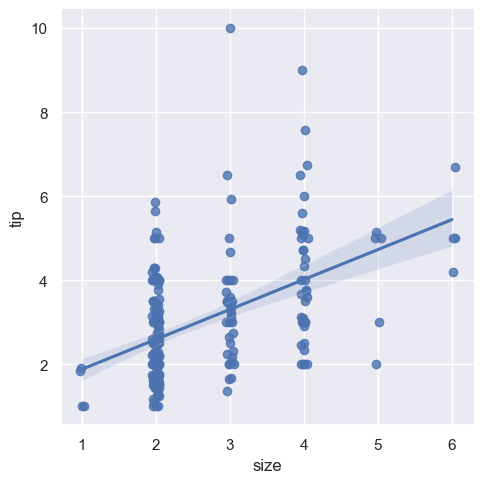
../_images/2eed646f76315f02e3c504d26a842449a46f4a5321d3b2f96b3de37dc2c6a1a6.png

tips_jittered = tips.copy()
tips_jittered["x_jittered"] = tips_jittered["size"] + np.random.uniform(-0.05, 0.05, size=len(tips_jittered))

fig = px.scatter(
    tips_jittered,
    x="x_jittered",
    y="tip",
    trendline="ols",
    template="plotly_white",
    title="Tip vs Table Size (with x_jitter = 0.05)"
)

fig.update_traces(marker=dict(size=7, opacity=0.6))
fig.show()

Drugą opcją jest “zwinięcie” obserwacji w każdym dyskretnym przedziale, aby wykreślić oszacowanie tendencji centralnej (w tym przypadku średniej) wraz z przedziałem ufności.

sns.lmplot(x="size", y="tip", data=tips, x_estimator=np.mean)

<seaborn.axisgrid.FacetGrid at 0x20baf7c9df0>

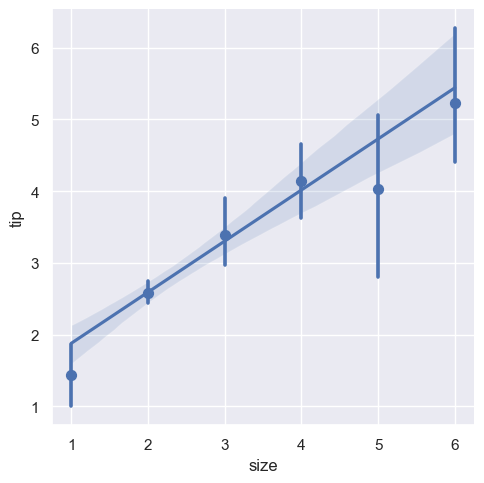
../_images/7b96bbc030c1fa816ffa8e9a9ad7d92c179038fee9e179f89ab908a15143c97d.png

tips_mean = tips.groupby("size", as_index=False)["tip"].mean()

fig = px.scatter(
    tips_mean,
    x="size",
    y="tip",
    trendline="ols",
    template="plotly_white",
    title="Mean Tip per Table Size (x_estimator = np.mean)"
)

fig.update_traces(marker=dict(size=10, color="royalblue"))

fig.show()

Żeby trochę lepiej odwzorować działanie seaborn’a można sobie rozrysować oryginalne dane w tle.

# Base figure with raw data (gray)
fig = go.Figure()
fig.add_trace(go.Scatter(
    x=tips["size"], y=tips["tip"],
    mode='markers',
    name='Raw data',
    marker=dict(color='lightgray', size=6, opacity=0.3)
))

# Add mean points
fig.add_trace(go.Scatter(
    x=tips_mean["size"], y=tips_mean["tip"],
    mode='markers',
    name='Mean per size',
    marker=dict(color='royalblue', size=10)
))

# Add regression line (fit on means)
coeffs = np.polyfit(tips_mean["size"], tips_mean["tip"], 1)
x_fit = np.linspace(tips_mean["size"].min(), tips_mean["size"].max(), 100)
y_fit = np.polyval(coeffs, x_fit)
fig.add_trace(go.Scatter(
    x=x_fit, y=y_fit,
    mode='lines',
    name='OLS fit (on means)',
    line=dict(color='red')
))

fig.update_layout(
    template='plotly_white',
    title='Tip vs Table Size (Mean per Size)',
    xaxis_title='Size',
    yaxis_title='Tip'
)

fig.show()

Wizualizacja z wykorzystaniem innych modeli#

Wizualizacja wielu relacji jednocześnie#

sns.jointplot(x="total_bill", y="tip", data=tips, kind="reg")

<seaborn.axisgrid.JointGrid at 0x20bae2b0140>

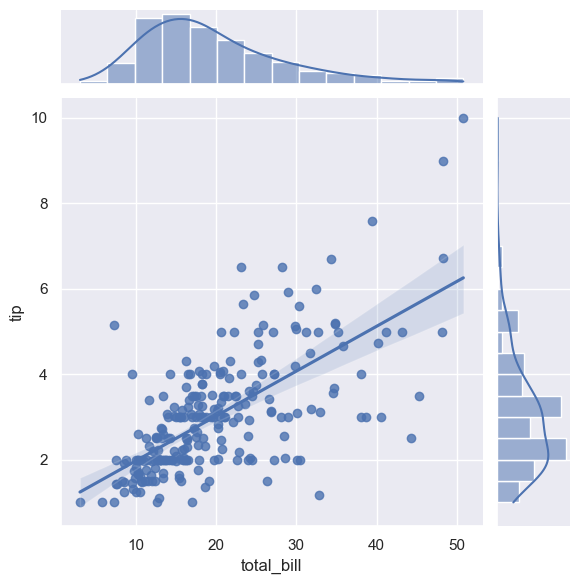
../_images/64dd5b92d892293ac7c621642d0b74f7f5019c7e3a35a9d099c68f3404f184e7.png

fig = px.scatter(
    tips,
    x="total_bill",
    y="tip",
    trendline="ols",
    marginal_x="histogram",
    marginal_y="histogram",
    template="plotly_white",
    title="Joint Distribution of Total Bill and Tip (with Regression)"
)

fig.show()

sns.pairplot(tips, x_vars=["total_bill", "size"], y_vars=["tip"],
             height=5, aspect=.8, kind="reg")

<seaborn.axisgrid.PairGrid at 0x20baf8fe0f0>

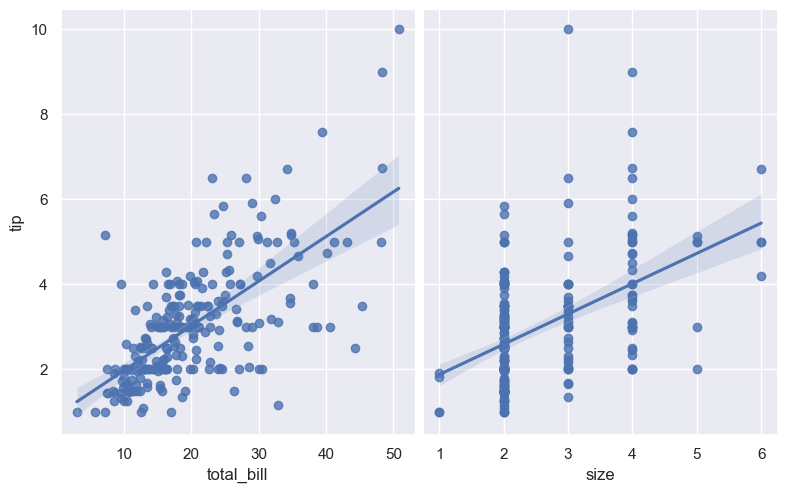
../_images/c256d41b61737cc04ac3dd0423b548000336f9c399b260d800b7d48466ed7318.png

x_vars = ["total_bill", "size"]

fig = make_subplots(rows=1, cols=len(x_vars), subplot_titles=x_vars)

for i, x in enumerate(x_vars, start=1):
    scatter = px.scatter(
        tips,
        x=x,
        y="tip",
        trendline="ols",
        template="plotly_white"
    )

    for trace in scatter.data:
        fig.add_trace(trace, row=1, col=i)

fig.update_layout(
    template="plotly_white",
    showlegend=False,
    title="Regression Plots of Tip vs Total Bill and Size"
)

fig.show()

Wizualizacja danych kategorycznych#

Powyższe metody wizulizacji skupiały się najczęściej na danych liczbowych, gdzie zmienna kategoryczna była nam potrzebna jedynie do grupowania czy agregowania naszych danych. W tej części skupimy się na metodach bezpośrednij wizualizacji zmiennej kategorycznej.

Zmienna kategoryczna w postaci wykresu punktowego#

Podstawową formą wizualizacji dla zmiennej katgorycznej jest wykres rozrzutu przedstawiający daną zmienną liczbową w zależności od zmiennej kategorycznej. Parametr kind == strip oznacza, że do zmiennej y dodawany jest pewinen element losowy w celu “rozrzucenia” obserwacji na osi y. Tak przedstawiony wykres może nam odpowiedzieć na pytania dotyczące rozkładu naszej zmiennej y wzlędem zmiennej x oraz może pomóc nam dostrzeć pewne anomalie w naszych danych.

sns.catplot(x="day", y="total_bill", kind="strip", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20baf97f1a0>

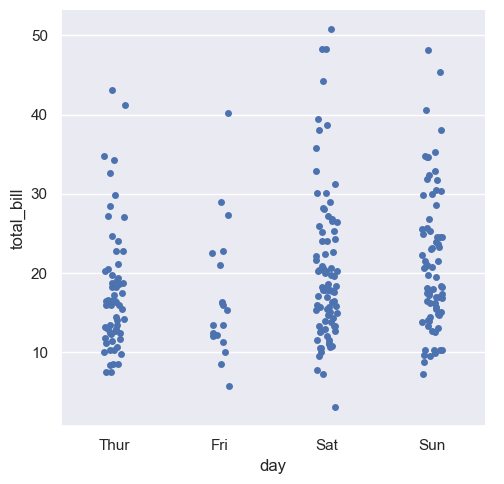
../_images/93d280ccc456c7feeec4d63bdecdc23013b38ffd3b7d1c4ac79d817c9dc8786b.png

fig = px.strip(
    tips,
    x="day",
    y="total_bill",
    category_orders={"day": ["Thur", "Fri", "Sat", "Sun"]},
    template="plotly_white",
    title="Total Bill by Day (Custom Order)"
)

fig.show()

Tak wykres wyglądałby w przypadku pominięcia dodawania składnika losowego do każdej obserwacji z osobna.

sns.catplot(x="day", y="total_bill", jitter=False, data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bafdca690>

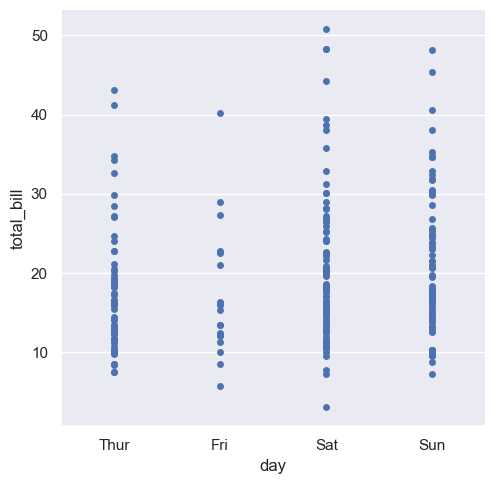
../_images/0e5304004f6e999deafa263de51b99a9f04cd199bfda2569e7e1df732a5a8614.png

fig = px.strip(
    tips,
    x="day",
    y="total_bill",
    category_orders={"day": ["Thur", "Fri", "Sat", "Sun"]},
    template="plotly_white",
    title="Total Bill by Day (No Jitter)"
)

fig.update_traces(jitter=0)  

fig.show()

Czasami dobrym pomysłem jest, także dodanie do wykresu kolejnego wymiaru (w tym przypadku płci). Może nam to pomoć zrozumieć kolejne relacje zachodzące w naszych danych.

sns.catplot(x="day", y="total_bill", hue="sex", kind="strip", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bb01aa1b0>

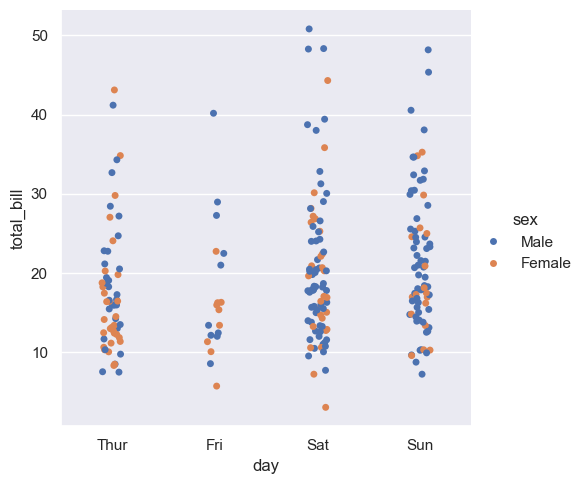
../_images/732464d0977d96e21c0fabb7baaeec949bd3a0fd025b1755b117f525c172830c.png

fig = px.strip(
    tips,
    x="day",
    y="total_bill",
    category_orders={"day": ["Thur", "Fri", "Sat", "Sun"]},
    template="plotly_white",
    title="Total Bill by Day (Custom Order)",
    color="sex"
)

fig.show()

Rozkład zmiennej w zależności od danych kategorycznych#

W poprzednich wizualizacjach pokazaliśmy w jaki sposób można zwizulizować histogram, a wieć wykres rozkładu naszej zmiennej w zależności od danych kategorycznych. Istnieją również innego rodzaju wykresy, które będące odpowiedzią na rozkład naszej zmiennej - wykresy pudełkowe.

Podstawowy wykres pudełkowy można uzyskać korzystając z matplotlib.

plt.boxplot(x=housing['MedHouseVal'])

{'whiskers': [<matplotlib.lines.Line2D at 0x20bb0289100>,
  <matplotlib.lines.Line2D at 0x20bb0340b60>],
 'caps': [<matplotlib.lines.Line2D at 0x20bb0343800>,
  <matplotlib.lines.Line2D at 0x20bb0343860>],
 'boxes': [<matplotlib.lines.Line2D at 0x20bb0288a70>],
 'medians': [<matplotlib.lines.Line2D at 0x20bb0342ae0>],
 'fliers': [<matplotlib.lines.Line2D at 0x20bb0340830>],
 'means': []}

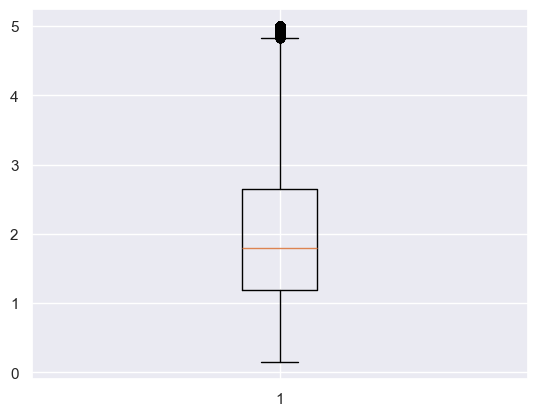
../_images/421d182cb3549bd0992945cf2454181e6d00466a09e653eca8a4a2d1601db6cf.png

Jednakże, tym samym małym wysiłkiem można uzyskać dużo ładniejszy wykres korzystając z API seaborn.

sns.catplot(y='MedHouseVal', data=housing, kind="box")

<seaborn.axisgrid.FacetGrid at 0x20bb028b2c0>

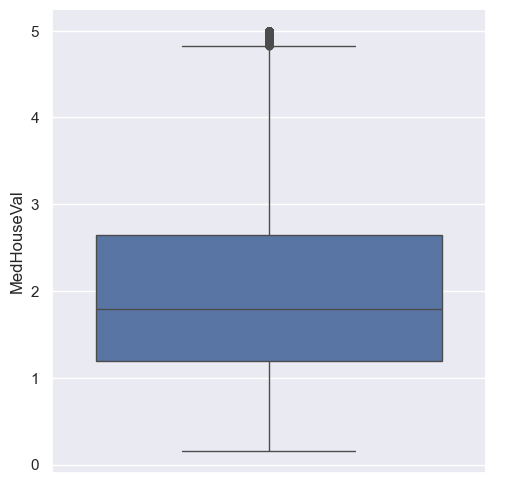
../_images/47d1f808a1e3db03f86ed479a723ace59e2d4a7a67cd742563e06ae2e9fb13bf.png

fig = px.box(
    housing,
    y='MedHouseVal',
    title='Box Plot of Median House Value',
    template="plotly_white"
)

fig.show()

sns.catplot(x="day", y="total_bill", kind="box", data=tips, hue="day")

<seaborn.axisgrid.FacetGrid at 0x20bb03274a0>

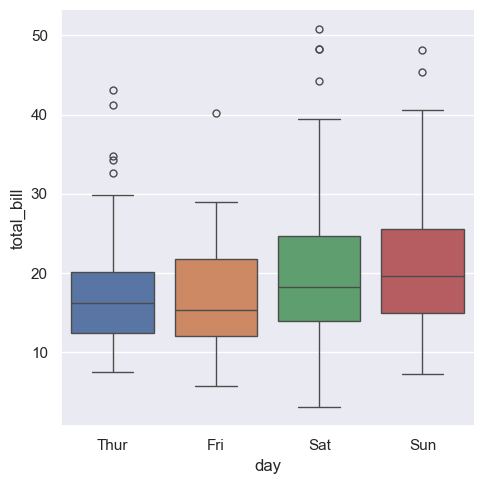
../_images/2cc5b3538556d365e021a6313af2b16cc270a4781e82df9188b3d556ba446273.png

fig = px.box(
    tips,
    y='total_bill',
    title='Box Plot of Total Bill by Day',
    template="plotly_white",
    x='day',
    category_orders={"day": ["Thur", "Fri", "Sat", "Sun"]},
)

fig.show()

sns.catplot(x="day", y="total_bill", hue="smoker", kind="box", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bb15dc530>

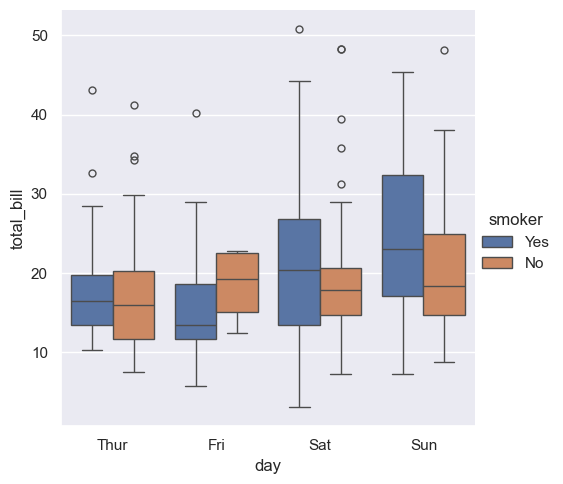
../_images/5663071f97a16c717c29de616b7986b71bb20e06aa7a9d245f27b205841eade1.png

fig = px.box(
    tips,
    y='total_bill',
    title='Box Plot of Total Bill by Day',
    template="plotly_white",
    x='day',
    category_orders={"day": ["Thur", "Fri", "Sat", "Sun"]},
    color='smoker'
)

fig.show()

Interpretacja wykresu pudełkowego jest dość prosta. Są w nim zawarte informacje na temat wartości minimalnej, kwartylu I, medianie, kwartylu III, wartości maksymalnej, a także o potencjalnych anomaliach wyliczonych za pomocą rozstępu między kwartylowego. Jednakże wykres pudełkowy można zastąpić innymi podobnymi wizualizacjami, którą czasami mogą okazać się bardzo pomocne.

sns.catplot(x="AveRooms_greater_5", y="MedHouseVal", kind="box",
            data=housing.sort_values("AveRooms_greater_5"), hue="AveRooms_greater_5")

<seaborn.axisgrid.FacetGrid at 0x20bb15c72f0>

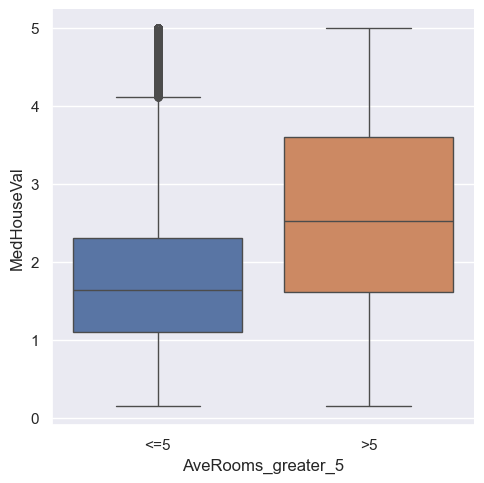
../_images/58ccd1c3f642d3ba2ae170343b44ba7558825a13a46da390e649728077d8f056.png

fig = px.box(
    housing.sort_values("AveRooms_greater_5"),
    x="AveRooms_greater_5",
    y="MedHouseVal",
    color="AveRooms_greater_5",
    template="plotly_white",
    title="Median House Value by AveRooms_greater_5"
)

fig.show()

Wykresem podobnym do wykresu pudełkowego - boxplot, ale zoptymalizowany pod kątem wyświetlania większej ilości informacji o kształcie rozkładu jest inny wykres pudełowy - boxenplot.

sns.catplot(x="AveRooms_greater_5", y="MedHouseVal", kind="boxen",
            data=housing.sort_values("AveRooms_greater_5"), hue="AveRooms_greater_5")

<seaborn.axisgrid.FacetGrid at 0x20bb15c4e60>

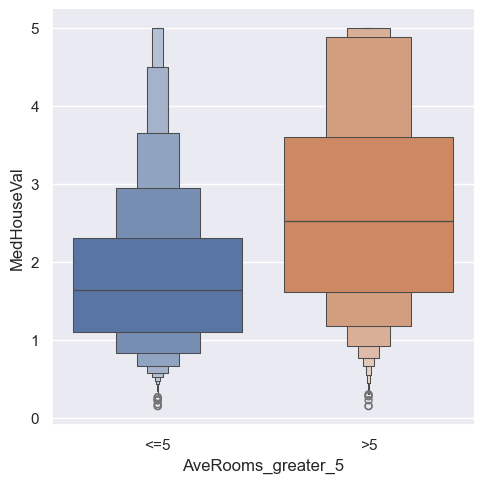
../_images/85e6d9de4a67f422686800fe122d9ee9842cd132cc3ef3615fec2e9df13fe778.png

Ciekawą oraz często wykorzystywana interpretacją rozkładu jest violinplot* łączący wykres pudełkowy z estymacją gęstości rozkładu. Jest on w stanie jeszcze dokładniej pomóc nam oszacować miejsca w których występują większe skupiska naszych obserwacji.

sns.catplot(x="AveRooms_greater_5", y="MedHouseVal", kind="violin",
            data=housing.sort_values("AveRooms_greater_5"), hue="AveRooms_greater_5")

<seaborn.axisgrid.FacetGrid at 0x20bb170b020>

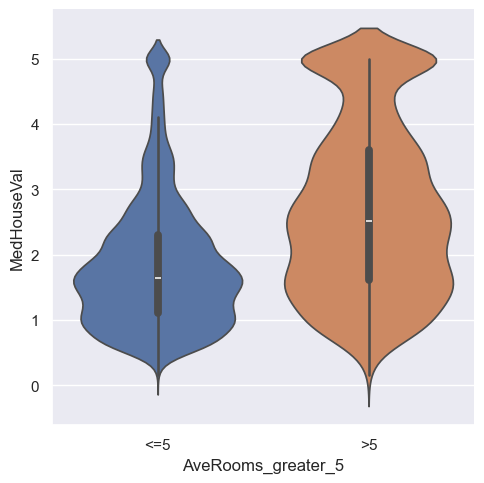
../_images/0fc69139269d977315e2b45a30cb11e7360fd441979d09e0a2527222f59bc490.png

fig = px.violin(
    housing.sort_values("AveRooms_greater_5"),
    x="AveRooms_greater_5",
    y="MedHouseVal",
    color="AveRooms_greater_5",
    box=True,
    template="plotly_white",
    title="Median House Value by AveRooms_greater_5"
)

fig.show()

Dobrym połączeniem jest violinplot z stripplot, czyli przedstawionym wcześniej wykresem rozrzutu. Jednakże w przypadku dużej ilości danych wizualizacja może się długo ładować.

g = sns.catplot(x="day", y="total_bill", kind="violin", inner=None, data=tips, hue="day")
sns.stripplot(x="day", y="total_bill", color="k", size=3, data=tips, ax=g.ax)

<Axes: xlabel='day', ylabel='total_bill'>

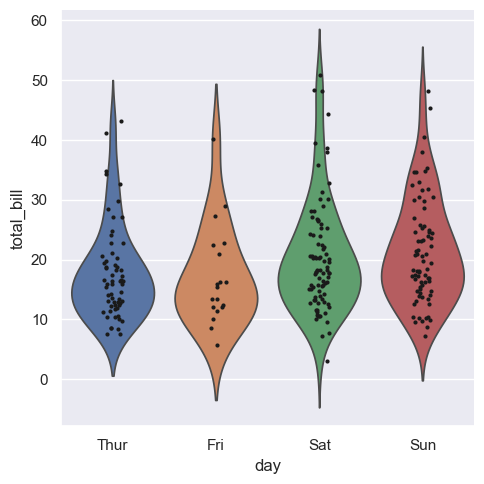
../_images/c1a443778bfd89edee392983d2e48f43d40a52a0dd8068105079268fde364ee4.png

fig = px.violin(
    tips,
    x="day",
    y="total_bill",
    color="day",
    box=False,
    points=False,
    template="plotly_white",
    category_orders={"day": ["Thur", "Fri", "Sat", "Sun"]}
)

strip = px.strip(
    tips,
    x="day",
    y="total_bill",
    category_orders={"day": ["Thur", "Fri", "Sat", "Sun"]}
)

for trace in strip.data:
    trace.update(marker=dict(color="black", size=3, opacity=0.6), showlegend=False)
    fig.add_trace(trace)

fig.update_layout(
    title="Total Bill by Day (Violin + Strip Overlay)",
    template="plotly_white"
)

fig.show()

Estymacja statystyczna w ramach zmiennej kategorycznej#

W pewnych przypadkach naszym celem może być oszacowanie tendencji centralnej dla naszych danych np. średniej czy mediany. Wtedy bardzo często korzysta się z wykresu słupkowego wraz z pewnym pozniomem ufności. W przypadku biblioteki seaborn narysowanie tego typu wykresu jest bardzo proste. Domyślnie tendecją centralną jest średnia arytmetyczna.

sns.catplot(x="sex", y="tip", hue="time", kind="bar", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bb0270920>

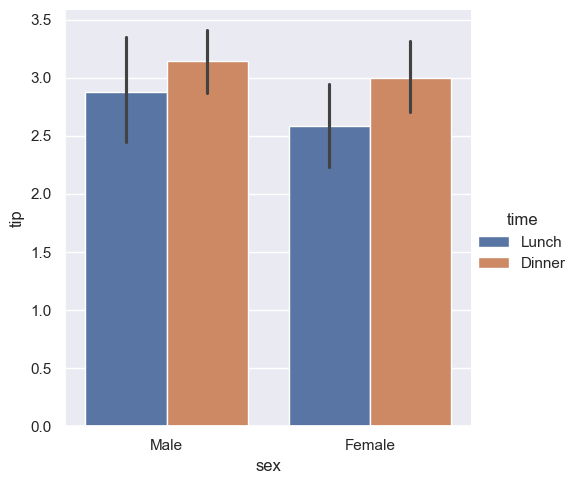
../_images/f7ade73d33d0d67c624191e999332a395a71403fc9636f1ad4b31978c8fabc16.png

group_stats = (
    tips.groupby(["sex", "time"])["tip"]
    .agg(["mean", "sem", "count"])
    .reset_index()
)
group_stats["ci95"] = group_stats["sem"] * stats.t.ppf(0.975, group_stats["count"] - 1)

fig = px.bar(
    group_stats,
    x="sex",
    y="mean",
    color="time",
    error_y="ci95",
    barmode="group",
    template="plotly_white",
    title="Average Tip by Sex and Time (95% CI)"
)

fig.update_layout(yaxis_title="Mean Tip")
fig.show()

C:\Users\knajmajer\AppData\Local\Temp\ipykernel_21120\2270018583.py:2: FutureWarning:

The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.

Szczególnym przypadkiem wykresu catplot jest wykres przedstawiający liczbę obserwacji przypadającą na daną kategorię.

sns.catplot(x="sex", kind="count", data=tips, hue='sex')

<seaborn.axisgrid.FacetGrid at 0x20bb16d8a70>

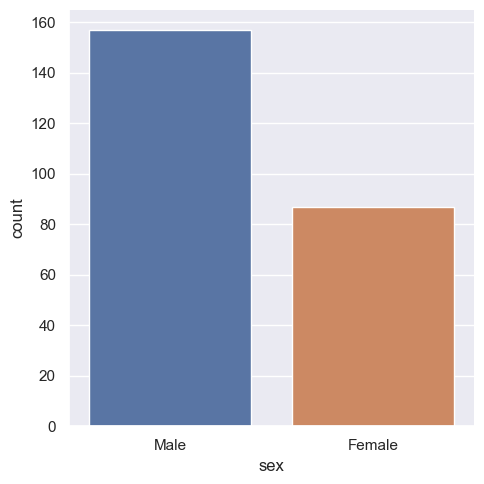
../_images/27519e3888c03b260825b858549d441f70cabe89b37882a53ed4ac9310d78f15.png

fig = px.histogram(
    tips,
    x="sex",
    color="sex",
    template="plotly_white",
    title="Count of Records by Sex"
)

fig.update_layout(
    barmode="group",
    showlegend=False
)

fig.show()

sns.catplot(y="sex", hue="time", palette="pastel",  kind="count", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bb17be840>

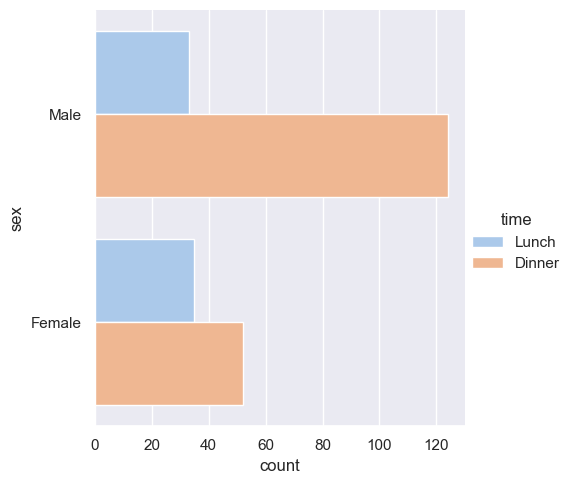
../_images/4709a9f2a84f24d04ebb2e45270e3ca6dc936e37e9372dc35e30302fd007a5c1.png

fig = px.histogram(
    tips,
    y="sex",
    color="time",
    template="plotly_white",
    title="Count of Records by Sex and Time",
    color_discrete_sequence=px.colors.qualitative.Pastel # nowa paleta kolorow
)

fig.update_layout(
    barmode="group",
    bargap=0.2
)

fig.show()

Inna formą wizualizacji może być, także pointplot, który te same relacje przedstawia w postaci wykresu punktowego, gdzie dany punkt przedstawia tendencję centralną danej kategorii natomiast pionowe linię określają przedział ufności. Atutem tego wykresu jest łączenie tych samych kategorii podanych w parametrze hue.

sns.catplot(x="sex", y="tip", hue="time", kind="point", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bb29f5040>

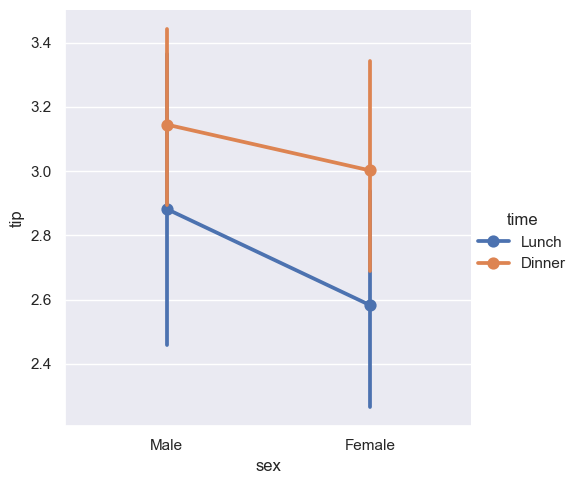
../_images/6d73bb3e586eeb645c0738f7bba75eb9cd0f973318339ab09943ca068a279ecc.png

group_stats = (
    tips.groupby(["sex", "time"])["tip"]
    .agg(["mean", "sem", "count"])
    .reset_index()
)
group_stats["ci95"] = group_stats["sem"] * stats.t.ppf(0.975, group_stats["count"] - 1)

fig = px.line(
    group_stats,
    x="sex",
    y="mean",
    color="time",
    error_y="ci95",
    markers=True,
    template="plotly_white",
    title="Mean Tip by Sex and Time (95% CI)"
)

fig.update_layout(yaxis_title="Mean Tip", xaxis_title="Sex")
fig.show()

C:\Users\knajmajer\AppData\Local\Temp\ipykernel_21120\3501454193.py:2: FutureWarning:

The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.

sns.catplot(x="size", y="tip", hue='sex', kind="point", data=tips)

<seaborn.axisgrid.FacetGrid at 0x20bb2fa4da0>

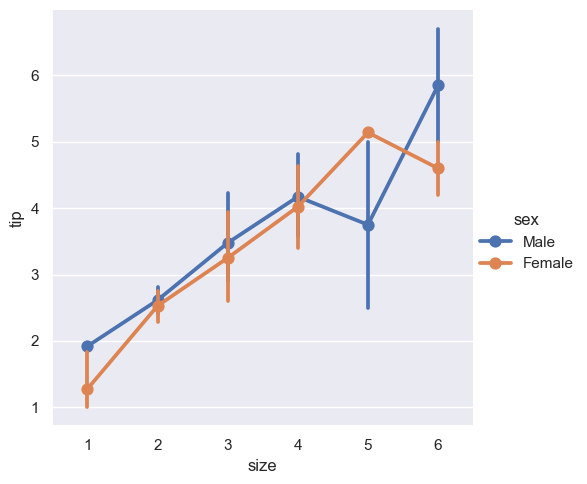
../_images/15d4cc489469bf32442a2e512d0ed860bc7c5a9fd7a3f289d7d73fd4440fbed0.png

Podsumowanie#

Wnioski:

Wykresy oparte o pandas lub matplotlib sprawdzają się w przypadku chęci zbudowania prostej wizualizacji podczas pierwszej fazy Eksploracyjnej analizy danych (Exploratory Data Analysis). Wykresy z rodziny seaborn oraz plotly dają większe możliwości, dzięki czemu możemy w ładniejszy sposób przedstawić nasze dane i wyciągnąć na ich podstawie istotne wnioski.

Zadanie#

Opierając się na powyższych wizualizacjach należy przeprowadzić eksploracyjną analizę danych dla tabeli Dane_Ladies. Dane należy zczytać z bazy SQL bezpośrednio do ramki danych (podpowiedź na samej górze notatnika).

Analiza powinna odpowiadać na kilka podstawowych pytań:

czy istnieje zależność jakiejś zmiennej liczbowej ze zmienną M2? (np. zależność od Transfer_Qty)
czy relacja ta jest w jakiś sposób zależna od zmiennej kategorycznej? (np. zależność od SLSU dla utworzonych grup Populacji lub od sezonu)
jaki jest rozkład poszczególnych zmiennych?

Do stworzenia wizualicji wykorzystaj przynajmniej raz pakietu seaborn i plotly (nie rób wszystkich wizualizacji w jednym pakiecie).

Do każdej wizualizacji napisz wnioski w Markdown. Możesz także policzyć statystyki opisowe (np. metoda description wywołana na ramce danych).

import pandas as pd
import sqlalchemy as sa

user = ""
password = ""

if user:

    connection_url = sa.engine.url.URL.create(
        "mssql+pyodbc",
        host="127.0.0.1,50001", # port after comma
        username=user,
        password=password,
        database="LPP_Workshop",
        query=dict(driver="ODBC Driver 17 for SQL Server")
    )
    engine = sa.create_engine(connection_url, fast_executemany=True)


    query = """
    SELECT top 1000 [STR_Nazwa]
        ,[Date]
        ,[M2]
        ,[EOPU]
        ,[SLSU]
        ,[TransferQty]
        ,[Population]
        ,[STR_TypeLoc]
        ,[Season]
        ,[SBCL_Nazwa]
        ,[CLA_Nazwa]
        ,[Class_1]
        ,[Class_2]
    FROM [LPP_Workshop].[dbo].[Dane_Ladies]
    """

    df = pd.read_sql(sa.text(query), engine.connect())

    df.head()
else:
    print("Podaj dane logowania")

Podaj dane logowania

df.info()

<class 'pandas.core.frame.DataFrame'>
Index: 5427 entries, 0 to 20636
Data columns (total 11 columns):
 #   Column              Non-Null Count  Dtype  
---  ------              --------------  -----  
 0   MedInc              5427 non-null   float64
 1   HouseAge            5427 non-null   float64
 2   AveRooms            5427 non-null   int32  
 3   AveBedrms           5427 non-null   int32  
 4   Population          5427 non-null   float64
 5   AveOccup            5427 non-null   float64
 6   Latitude            5427 non-null   float64
 7   Longitude           5427 non-null   float64
 8   MedHouseVal         5427 non-null   float64
 9   AveRooms_greater_5  5427 non-null   object 
 10  MedInc_greater_5    5427 non-null   object 
dtypes: float64(7), int32(2), object(2)
memory usage: 466.4+ KB

df.select_dtypes(include=['int64', 'float64']).columns.tolist()

['MedInc',
 'HouseAge',
 'Population',
 'AveOccup',
 'Latitude',
 'Longitude',
 'MedHouseVal']

df.describe()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude	MedHouseVal
count	5427.000000	5427.000000	5427.000000	5427.000000	5427.000000	5427.000000	5427.000000	5427.000000	5427.000000
mean	5.642734	24.006265	6.970149	0.921504	1398.071310	3.065282	35.813416	-119.645692	2.697583
std	2.310443	12.387420	4.006610	0.956342	1294.507464	7.540270	2.187464	2.069922	1.312575
min	0.499900	1.000000	6.000000	0.000000	5.000000	0.692308	32.570000	-124.350000	0.149990
25%	4.164300	15.000000	6.000000	1.000000	707.000000	2.581017	33.900000	-121.870000	1.617000
50%	5.396300	22.000000	6.000000	1.000000	1071.000000	2.861789	34.710000	-119.090000	2.518000
75%	6.676400	33.000000	7.000000	1.000000	1655.500000	3.178836	37.800000	-117.850000	3.606000
max	15.000100	52.000000	141.000000	34.000000	16305.000000	502.461538	41.860000	-114.310000	5.000010

sns.relplot(data=df, x='HouseAge', y='MedHouseVal')

<seaborn.axisgrid.FacetGrid at 0x20bb425b2c0>

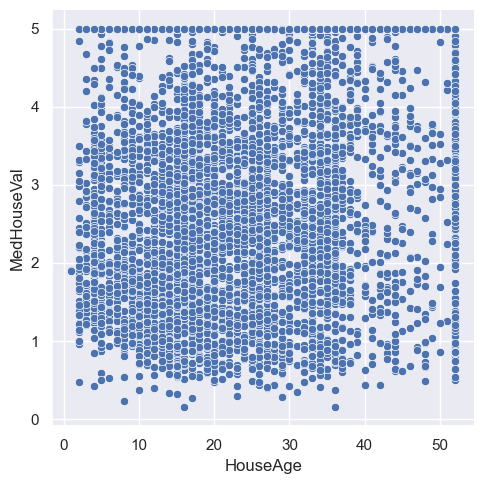
../_images/7dc11ba374031601542f73b776ef2bb50264d7ed28ee78abc4072aa37e056962.png

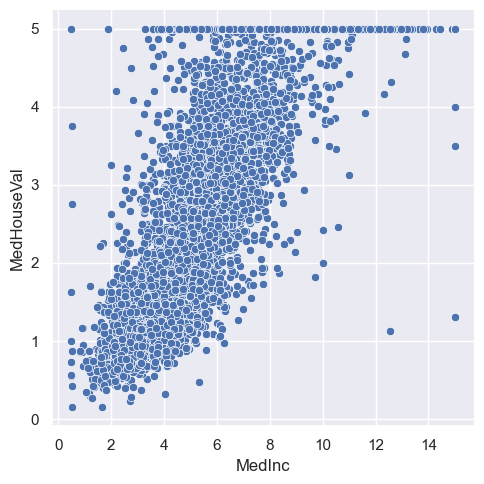
sns.relplot(data=df, x='MedInc', y='MedHouseVal')

<seaborn.axisgrid.FacetGrid at 0x20bb42baf00>

../_images/4965c064d71dfd356eebf5d94c197fa0f80a30e3b25bac7d467bf08fe2524409.png

px.scatter(df, x='AveOccup', y='HouseAge')

import plotly
plotly.offline.init_notebook_mode(connected=True)

import plotly.io as pio
pio.renderers.default = 'plotly_mimetype'

px.scatter(df, x='AveBedrms', y='MedInc')

# sns.relplot(df, x='M2', y='MedHouseVal', hue='Population')

# sns.relplot(x="M2", y="SLSU", data=df, hue='Season')

# px.scatter(df, x='M2', y='SLSU', color='Population')

df.info()

<class 'pandas.core.frame.DataFrame'>
Index: 5427 entries, 0 to 20636
Data columns (total 11 columns):
 #   Column              Non-Null Count  Dtype  
---  ------              --------------  -----  
 0   MedInc              5427 non-null   float64
 1   HouseAge            5427 non-null   float64
 2   AveRooms            5427 non-null   int32  
 3   AveBedrms           5427 non-null   int32  
 4   Population          5427 non-null   float64
 5   AveOccup            5427 non-null   float64
 6   Latitude            5427 non-null   float64
 7   Longitude           5427 non-null   float64
 8   MedHouseVal         5427 non-null   float64
 9   AveRooms_greater_5  5427 non-null   object 
 10  MedInc_greater_5    5427 non-null   object 
dtypes: float64(7), int32(2), object(2)
memory usage: 466.4+ KB

sns.displot(df, x='MedHouseVal', kde=True)

<seaborn.axisgrid.FacetGrid at 0x20bb44b9e20>

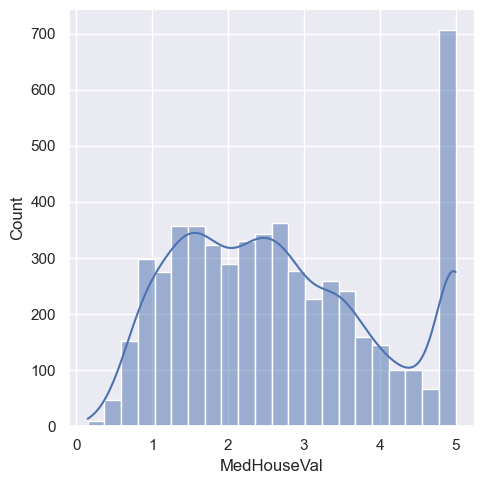
../_images/06ffed87bfd2f6a0cfd0b82a8a0e0f78837106a81d85e6027f7ce13212d23eb7.png

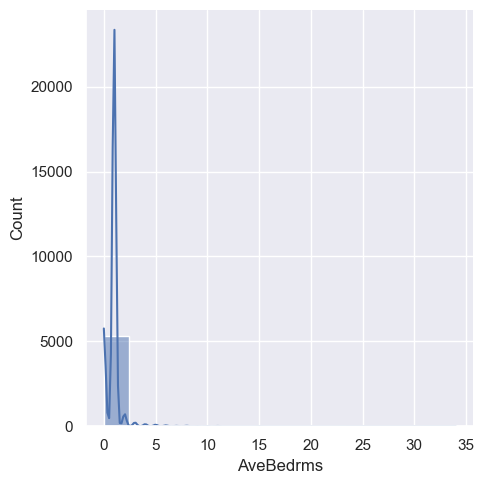
sns.displot(df, x='AveBedrms', kde=True)

<seaborn.axisgrid.FacetGrid at 0x20bb459ff20>

../_images/e5862d3194b6541ddb1de02d7681e9a676050e24890447c33b9211c6f7cb4627.png

df.info()

<class 'pandas.core.frame.DataFrame'>
Index: 5427 entries, 0 to 20636
Data columns (total 11 columns):
 #   Column              Non-Null Count  Dtype  
---  ------              --------------  -----  
 0   MedInc              5427 non-null   float64
 1   HouseAge            5427 non-null   float64
 2   AveRooms            5427 non-null   int32  
 3   AveBedrms           5427 non-null   int32  
 4   Population          5427 non-null   float64
 5   AveOccup            5427 non-null   float64
 6   Latitude            5427 non-null   float64
 7   Longitude           5427 non-null   float64
 8   MedHouseVal         5427 non-null   float64
 9   AveRooms_greater_5  5427 non-null   object 
 10  MedInc_greater_5    5427 non-null   object 
dtypes: float64(7), int32(2), object(2)
memory usage: 466.4+ KB

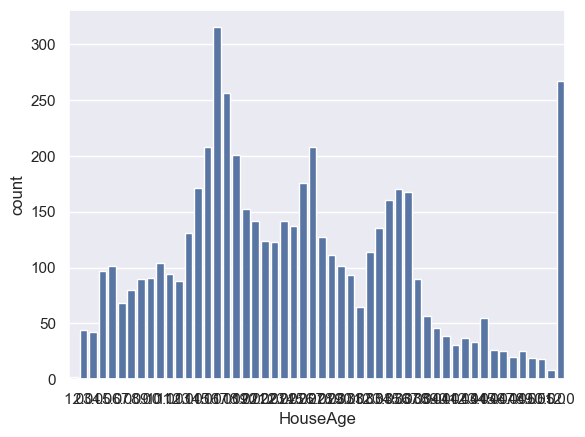
sns.countplot(x='HouseAge', data=df)

<Axes: xlabel='HouseAge', ylabel='count'>

../_images/61a08bbdedb67d489e274557ee87ed9ef71898023e2f2a7f49ec24ae9e6cf3af.png

Wizualizacja danych w Python

Contents

Wizualizacja danych w Python#

Odpytanie bazy z poziomu kodu#

Wstęp#

Biblioteki#

Przygotowanie danych#

Housing#

Fmri#

Tips#

Anscombe#

Wizualizacja zależności statystycznych#

Badanie relacji między zmiennymi przy użyciu wykresu punktowego#

Podkreślenie relacji liniowych między zmiennymi#

Wizualizacja w przypadku agregacji danych#

Prezentaja wielu relacji na róznych polach wykresu#

Wizualizacja rozkładu zmiennych#

Rozkład zmiennej jednowymiarowej#

Wizualizacja zmiennych kategorycznych#

Rozkład warunkowy względem innych zmiennych#

Gęstość rozkładu#

Dystrybuanta rozkładu#

Rozkład wielowymiarowy#

Wizualizacja modeli regresyjnych#

Wizualizacja regresji liniowej#

Wizualizacja z wykorzystaniem innych modeli#

Wizualizacja wielu relacji jednocześnie#

Wizualizacja danych kategorycznych#

Zmienna kategoryczna w postaci wykresu punktowego#

Rozkład zmiennej w zależności od danych kategorycznych#

Estymacja statystyczna w ramach zmiennej kategorycznej#

Podsumowanie#

Zadanie#