Czyszczenie danych#
Czyszczenie danych jest to proces polegający na identyfikacji i naprawie różnego rodzaju błędów w danych.
Czyszczenie danych obejmuje zazwyczaj następujące elementy:
czyszczenie formatów danych
czyszczenie kodowania zmiennych kategorycznych
czyszczenie nieprawidłowych wartości zmiennych numerycznych
czyszczenie wartości odstających
usuwanie duplikatów
imputacja wartości brakujących
Czyszczenie danych stanowi jeden z ważniejszych etapów w procesie budowy modeli uczenia maszynowego, dlatego należy mu poświęcić dużo uwagi. Zazwyczaj stanowi też jedną z najbardziej czasochłonnych faz i może wymagać czasem wielu iteracji polegających na identyfikacji i naprawie kolejnych nieprawidłowości, a następnie analizy impaktu zmian na wyniki modelu. Należy również pamiętać, że czyszczenie danych musi być poprzedzone ich dobrym zrozumieniem, inaczej nie będzie możliwe uzyskanie danych poprawnych pod kątem logiki biznesowej.
W tym notebooku przedstawione zostaną 2 przypadki - czyszczenie danych tabularycznych oraz czyszczenie szeregu czasowego. Najpierw jednak import bibliotek i wygenerowanie danych.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
Wygenerowanie danych#
Posłużymy się tutaj dwoma przykładami danych wymagających wyczyszczenia - danymi tabularycznymi reprezentującymi dane pacjentów oraz szeregiem czasowym pokazującym sprzedaż produktu o silnej sezonowości.
def generate_ts_data(month_coef=100, week_coef=10, day_coef=1, random_coef =10000):
dates = pd.date_range(start="2016-01-01", end="2020-12-31", freq ="D")
df = pd.DataFrame(dates, columns=["SalesDate"])
df["Month"] = df.SalesDate.dt.month
df["Week"] = df.SalesDate.dt.isocalendar().week
df["Year"] = df.SalesDate.dt.year
df["WeekDay"] = df.SalesDate.dt.dayofweek+1
df["SLSU"] = ((np.power(6.5-df.Month,2))*month_coef + (np.power(26.5-df.Week,2))*week_coef +df.WeekDay*day_coef)*np.sqrt(df["Year"]-df["Year"].min()+1)
df["SLSU"] = np.where((df["SalesDate"]>="2019-11-01")&(df["SalesDate"]<="2020-03-01"), 0, (df["SLSU"]))
df["SLSU"] = df["SLSU"] + np.random.choice(a=[0,df["SLSU"].max()*0.2], size=len(df),p=[0.998, 0.002])
return df.loc[:,["SalesDate","SLSU"]]
def generate_tabular_data(len_data=300):
id = range(len_data)
age = np.random.randint(low=5,high=100,size=len_data)
weight = np.round(np.random.normal(loc=60,scale=10,size=len_data))
height = np.round(np.random.normal(loc=160,scale=12,size=len_data))
bmi = np.round(weight/(height/100)**2,1)
city = np.random.choice(["Gdańsk","Gdynia", "Wejherowo", "Kościerzyna","Gdansk", "Koscierzyna"], p=[0.4, 0.2, 0.1, 0.1, 0.1, 0.1], size=len_data)
num_covid_tests = np.random.randint(low=0,high=5,size=len_data)
num_positive_tests = (num_covid_tests - num_covid_tests *np.random.choice(np.arange(6),p=[0.65, 0.2, 0.1, 0.02, 0.02, 0.01], size=len_data)).astype(int) + np.random.choice(a=[0,1], size=len_data,p=[0.9, 0.1])
sex = np.random.choice(["M", "F", "N"], size=len_data, p=[0.45, 0.45, 0.1])
dict_data = {"unique_id":id, "age":age, "weight":weight, "height":height, "bmi":bmi, "city":city,
"num_covid_tests":num_covid_tests, "num_positive_tests":num_positive_tests, "sex":sex}
df = pd.DataFrame(dict_data)
df["num_covid_tests"] = np.where(df["num_covid_tests"]==0, np.nan, df["num_covid_tests"])
df["weight"] = df["weight"].astype(str)
df["height"] = df["height"] * np.random.choice([1,2], p =[0.99, 0.01], size=len_data)
df["bmi"] = df["bmi"] * np.random.choice([1,np.random.rand()], p =[0.9, 0.1], size=len_data)
df["age"] = np.where(df["age"]>65,np.nan, df["age"])
df["city"] = np.select([df["bmi"]>30,df["bmi"]<=20, df["bmi"]<=30],[df["city"].str.lower(), df["city"].str.upper(), df["city"]])
return pd.concat([df, df.sample(frac=0.05)])
Czyszczenie danych tabularycznych#
df =generate_tabular_data(len_data=300)
Pierwszym krokiem w czyszczeniu danych powinno zawsze być przyjrzenie się wycinkowi danych oraz podstawowym informacjom o naszej ramce danych:
df.head()
| unique_id | age | weight | height | bmi | city | num_covid_tests | num_positive_tests | sex | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | NaN | 62.0 | 150.0 | 27.6 | Kościerzyna | NaN | 0 | M |
| 1 | 1 | 23.0 | 59.0 | 160.0 | 23.0 | Gdańsk | NaN | 1 | F |
| 2 | 2 | NaN | 56.0 | 155.0 | 23.3 | Gdansk | NaN | 0 | F |
| 3 | 3 | 35.0 | 58.0 | 145.0 | 27.6 | Gdynia | NaN | 0 | M |
| 4 | 4 | NaN | 55.0 | 148.0 | 25.1 | Kościerzyna | 3.0 | 3 | F |
df.info()
<class 'pandas.core.frame.DataFrame'>
Index: 315 entries, 0 to 209
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 315 non-null int64
1 age 190 non-null float64
2 weight 315 non-null object
3 height 315 non-null float64
4 bmi 315 non-null float64
5 city 315 non-null object
6 num_covid_tests 238 non-null float64
7 num_positive_tests 315 non-null int32
8 sex 315 non-null object
dtypes: float64(4), int32(1), int64(1), object(3)
memory usage: 23.4+ KB
Formaty danych#
Najczęściej występującym problemem jest formatowanie zmiennych numerycznych jako kategorycznych, tutaj widzimy to np. dla zmiennej weight, może to wynikać również z nieprawidłowych wartości występujących w takich kolumnach.
df.select_dtypes("object")
| weight | city | sex | |
|---|---|---|---|
| 0 | 62.0 | Kościerzyna | M |
| 1 | 59.0 | Gdańsk | F |
| 2 | 56.0 | Gdansk | F |
| 3 | 58.0 | Gdynia | M |
| 4 | 55.0 | Kościerzyna | F |
| ... | ... | ... | ... |
| 282 | 52.0 | Koscierzyna | F |
| 267 | 54.0 | GDYNIA | N |
| 31 | 51.0 | KOSCIERZYNA | F |
| 49 | 53.0 | KOSCIERZYNA | F |
| 209 | 71.0 | Gdynia | N |
315 rows × 3 columns
df.select_dtypes("float64")
| age | height | bmi | num_covid_tests | |
|---|---|---|---|---|
| 0 | NaN | 150.0 | 27.6 | NaN |
| 1 | 23.0 | 160.0 | 23.0 | NaN |
| 2 | NaN | 155.0 | 23.3 | NaN |
| 3 | 35.0 | 145.0 | 27.6 | NaN |
| 4 | NaN | 148.0 | 25.1 | 3.0 |
| ... | ... | ... | ... | ... |
| 282 | 55.0 | 145.0 | 24.7 | NaN |
| 267 | NaN | 165.0 | 19.8 | 4.0 |
| 31 | 20.0 | 164.0 | 19.0 | 4.0 |
| 49 | 55.0 | 167.0 | 19.0 | 2.0 |
| 209 | 41.0 | 171.0 | 24.3 | 1.0 |
315 rows × 4 columns
Ponadto niektóre z powyższych zmiennych np. num_covid_tests wydają się bardziej pasować do formatu int niż float, jednak należy pamiętać, że zmienne zawierające brakujące wartości są automatycznie konwertowane na format float, dlatego na razie ograniczymy się do konwersji dla zmiennej weight.
columns_to_convert = ["weight"]
df[columns_to_convert] = df[columns_to_convert].astype("float64")
df.info()
<class 'pandas.core.frame.DataFrame'>
Index: 315 entries, 0 to 209
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 315 non-null int64
1 age 190 non-null float64
2 weight 315 non-null float64
3 height 315 non-null float64
4 bmi 315 non-null float64
5 city 315 non-null object
6 num_covid_tests 238 non-null float64
7 num_positive_tests 315 non-null int32
8 sex 315 non-null object
dtypes: float64(5), int32(1), int64(1), object(2)
memory usage: 23.4+ KB
Atrybuty zmiennych kategorycznych#
Zmienne kategoryczne są szczególnie narażone na błędy wynikające z literówek lub nieprawidłowego kodowania, co prowadzi do błędnego zwiększenia liczby ich unikalnych atrybutów. Można to zaobserwować dla przedstawionych poniżej zmiennych:
for column in df.select_dtypes("object").columns.tolist():
print("*"*20)
print(column.upper())
print("*"*20)
print(df[column].value_counts())
********************
CITY
********************
city
Gdańsk 60
GDAŃSK 40
Gdynia 34
Gdansk 26
Kościerzyna 24
Wejherowo 20
Koscierzyna 17
KOSCIERZYNA 17
gdańsk 14
GDYNIA 13
KOŚCIERZYNA 8
WEJHEROWO 8
gdynia 8
GDANSK 8
gdansk 6
kościerzyna 5
wejherowo 4
koscierzyna 3
Name: count, dtype: int64
********************
SEX
********************
sex
F 146
M 134
N 35
Name: count, dtype: int64
Jak widać zmienna city jest obarczona licznymi błędami wynikającymi z literówek oraz używania róznej wielkości liter. Tutaj błędy mogą stosunkowo łatwo zostać naprawione, jednak najczęściej do takiej poprawy niezbędna jest wiedza biznesowa odnośnie tego jakie atrybuty powinna dana zmienna posiadać i co one oznaczają.
df["city"] = df["city"].str.capitalize()
df["city"] = df["city"].replace({"Gdansk":"Gdańsk", "Koscierzyna":"Kościerzyna"})
df["city"].value_counts()
city
Gdańsk 154
Kościerzyna 74
Gdynia 55
Wejherowo 32
Name: count, dtype: int64
W przypadku zmiennej oznaczającej płeć pacjenta poza oczekiwanymi atrybutami M i F występuje jeszcze jedno oznaczenie - N. Przy założeniu, że nie ma żadnych wytycznych biznesowych określających, że taka wartość w tej kolumnie oznacza np. brak danych, musimy potraktować tą wartość jako błędną i oznaczyć jako brakującą. Tutaj zamienimy tę wartość na pustą, a wypełnieniem jej zajmiemy się w kolejnych sekcjach.
df["sex"] = np.where(df["sex"]=="N",np.nan, df["sex"])
df["sex"].value_counts(dropna=False)
sex
F 146
M 134
NaN 35
Name: count, dtype: int64
Weryfikacja duplikatów#
Kolejnym istotnym krokiem jest weryfikacja czy w danych nie występują duplikaty. Aby zbadać występowanie duplikatów dla danych niezbędna jest wiedza jakie kolumny wyznaczają unikalne kombinacje. W tym wypadku zakładamy, że odpowiada za to kolumna unique_id, zatem wystarczy porównać liczbę jej unikalnych wartości z liczebnością ramki danych.
df["unique_id"].nunique(), df.shape[0]
(300, 315)
Jak widać w danych występują duplikaty, do ich usunięcia najprościej wykorzystać funkcję drop_duplicates, wybierając jako subset unique_id. Funkcja daje również możliwość wyboru, który rekord zachować przy wykryciu duplikatów, załóżmy, że tutaj interesuje nas ostatni rekord bo reprezentuje np. najnowszy wpis w danych.
df = df.drop_duplicates(subset=["unique_id"], keep='last')
df.info()
<class 'pandas.core.frame.DataFrame'>
Index: 300 entries, 0 to 209
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 300 non-null int64
1 age 179 non-null float64
2 weight 300 non-null float64
3 height 300 non-null float64
4 bmi 300 non-null float64
5 city 300 non-null object
6 num_covid_tests 226 non-null float64
7 num_positive_tests 300 non-null int32
8 sex 269 non-null object
dtypes: float64(5), int32(1), int64(1), object(2)
memory usage: 22.3+ KB
Sprawdzanie zmiennych numerycznych#
Kolejnym krokiem jest czyszczenie zmiennych numerycznych, co obejmować będzie identyfikację i naprawianie wartości nieprawidłowych z punktu widzenia logiki biznesowej oraz wartości odstających.
df.describe()
| unique_id | age | weight | height | bmi | num_covid_tests | num_positive_tests | |
|---|---|---|---|---|---|---|---|
| count | 300.000000 | 179.000000 | 300.000000 | 300.000000 | 300.000000 | 226.000000 | 300.000000 |
| mean | 149.500000 | 34.251397 | 59.103333 | 160.403333 | 23.375241 | 2.553097 | 0.920000 |
| std | 86.746758 | 17.207538 | 10.170420 | 16.182715 | 5.677438 | 1.138933 | 2.450909 |
| min | 0.000000 | 5.000000 | 34.000000 | 128.000000 | 10.063127 | 1.000000 | -16.000000 |
| 25% | 74.750000 | 19.000000 | 53.000000 | 151.000000 | 19.100000 | 2.000000 | 0.000000 |
| 50% | 149.500000 | 36.000000 | 59.000000 | 160.000000 | 23.050000 | 3.000000 | 1.000000 |
| 75% | 224.250000 | 46.000000 | 65.250000 | 167.000000 | 26.700000 | 4.000000 | 3.000000 |
| max | 299.000000 | 65.000000 | 90.000000 | 316.000000 | 39.200000 | 4.000000 | 5.000000 |
Analizując powyższe statystyki dla zmiennych numerycznych możemy łatwo zauważyć występowanie wartości nieprawidłowych w postaci ujemnych wartości dla zmiennej num_positive_tests, która z założenia powinna być nieujemna. Ponadto można tutaj łatwo zauważyć występowanie wartości odstających dla zmiennej height. Dokładny proces identyfikacji wartości odstających został bardziej szczegółowo omówiony w osobnym notebooku, zatem tutaj ograniczymy się do oznaczenia takich wartosci jako brakujące, przyjmując arbitralnie wielkość progu.
df["height"] = np.where(df["height"]>=230,np.nan, df["height"])
df["num_positive_tests"] = np.where(df["num_positive_tests"]<0,np.nan, df["num_positive_tests"])
df.describe()
| unique_id | age | weight | height | bmi | num_covid_tests | num_positive_tests | |
|---|---|---|---|---|---|---|---|
| count | 300.000000 | 179.000000 | 300.000000 | 298.000000 | 300.000000 | 226.000000 | 269.000000 |
| mean | 149.500000 | 34.251397 | 59.103333 | 159.493289 | 23.375241 | 2.553097 | 1.490706 |
| std | 86.746758 | 17.207538 | 10.170420 | 11.674959 | 5.677438 | 1.138933 | 1.570753 |
| min | 0.000000 | 5.000000 | 34.000000 | 128.000000 | 10.063127 | 1.000000 | 0.000000 |
| 25% | 74.750000 | 19.000000 | 53.000000 | 151.000000 | 19.100000 | 2.000000 | 0.000000 |
| 50% | 149.500000 | 36.000000 | 59.000000 | 160.000000 | 23.050000 | 3.000000 | 1.000000 |
| 75% | 224.250000 | 46.000000 | 65.250000 | 167.000000 | 26.700000 | 4.000000 | 3.000000 |
| max | 299.000000 | 65.000000 | 90.000000 | 190.000000 | 39.200000 | 4.000000 | 5.000000 |
Relacje pomiędzy zmiennymi#
Oprócz analizy pojedynczych zmiennych czyszczenie danych powinno obejmować również analizę relacji logicznych pomiędzy poszczególnymi zmiennymi, wynikające z logiki biznesowej. Takie relacje mogą obejmować zarówno zestawienie wartości pojedynczych zmiennych jak i weryfikacje zmiennych wyliczanych na ich podstawie.
Przykładem takiej relacji w poniższych danych są zmienne num_covid_tests i num_positive_tests, za nieprawidłowe należy uznać wszystkie rekordy, dla których ta pierwsza zmienna jest mniejsza od drugiej.
df[df["num_covid_tests"]<df["num_positive_tests"]]
| unique_id | age | weight | height | bmi | city | num_covid_tests | num_positive_tests | sex | |
|---|---|---|---|---|---|---|---|---|---|
| 61 | 61 | NaN | 48.0 | 162.0 | 16.296923 | Gdańsk | 4.0 | 5.0 | NaN |
| 122 | 122 | NaN | 56.0 | 165.0 | 20.600000 | Gdańsk | 3.0 | 4.0 | F |
| 125 | 125 | 29.0 | 66.0 | NaN | 34.700000 | Gdańsk | 4.0 | 5.0 | F |
| 131 | 131 | NaN | 60.0 | 163.0 | 22.600000 | Kościerzyna | 3.0 | 4.0 | M |
| 166 | 166 | 43.0 | 61.0 | 142.0 | 30.300000 | Gdynia | 3.0 | 4.0 | NaN |
| 202 | 202 | NaN | 70.0 | 186.0 | 20.200000 | Gdańsk | 3.0 | 4.0 | M |
| 207 | 207 | 38.0 | 55.0 | 178.0 | 17.400000 | Gdańsk | 1.0 | 2.0 | F |
| 215 | 215 | NaN | 57.0 | 138.0 | 29.900000 | Kościerzyna | 4.0 | 5.0 | F |
| 217 | 217 | 17.0 | 53.0 | 175.0 | 15.406381 | Gdynia | 3.0 | 4.0 | M |
| 229 | 229 | 43.0 | 52.0 | 169.0 | 18.200000 | Gdańsk | 2.0 | 3.0 | F |
| 231 | 231 | 45.0 | 56.0 | 158.0 | 22.400000 | Kościerzyna | 3.0 | 4.0 | M |
| 233 | 233 | NaN | 65.0 | 160.0 | 25.400000 | Gdańsk | 3.0 | 4.0 | F |
| 264 | 264 | 5.0 | 67.0 | 148.0 | 30.600000 | Kościerzyna | 1.0 | 2.0 | M |
| 268 | 268 | NaN | 58.0 | 142.0 | 28.800000 | Gdańsk | 1.0 | 2.0 | M |
| 294 | 294 | 36.0 | 63.0 | 166.0 | 22.900000 | Wejherowo | 4.0 | 5.0 | F |
| 120 | 120 | NaN | 63.0 | 163.0 | 23.700000 | Wejherowo | 4.0 | 5.0 | F |
Przy założeniu, że wiemy iż bardziej wiarygodne są zapisy wartości zmiennej num_covid_tests można dokonać poprawy jak poniżej, alternatywą byłoby przypisanie takim przypadkom wartości pustej dla zmiennej num_positive_tests, ewentualnie usunięcie takich rekordów.
df["num_positive_tests"] = np.where(df["num_positive_tests"]>df["num_covid_tests"], df["num_covid_tests"], df["num_positive_tests"])
df[df["num_covid_tests"]<df["num_positive_tests"]]
| unique_id | age | weight | height | bmi | city | num_covid_tests | num_positive_tests | sex |
|---|
Zmienną wyliczoną na podstawie innych zmiennych reprezentuje tutaj bmi, znając formułę można zweryfikować czy wszędzie jest ona wyliczona prawidłowo:
df.loc[np.round(df["bmi"])!=np.round(df["weight"]/(df["height"]/100)**2)]
| unique_id | age | weight | height | bmi | city | num_covid_tests | num_positive_tests | sex | |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 5 | NaN | 68.0 | 147.0 | 31.500000 | Kościerzyna | 1.0 | NaN | F |
| 7 | 7 | NaN | 49.0 | 183.0 | 13.001917 | Gdańsk | 3.0 | 0.0 | F |
| 8 | 8 | NaN | 57.0 | 147.0 | 23.510315 | Wejherowo | 2.0 | 2.0 | F |
| 9 | 9 | 17.0 | 65.0 | 169.0 | 20.304363 | Gdynia | NaN | 0.0 | F |
| 13 | 13 | NaN | 54.0 | 150.0 | 21.373014 | Gdańsk | 4.0 | NaN | F |
| 24 | 24 | 44.0 | 57.0 | 144.0 | 27.500000 | Wejherowo | NaN | 0.0 | M |
| 29 | 29 | NaN | 45.0 | 141.0 | 20.126254 | Kościerzyna | 3.0 | 3.0 | F |
| 46 | 46 | 51.0 | 59.0 | 139.0 | 30.500000 | Gdańsk | 1.0 | 1.0 | M |
| 50 | 50 | 25.0 | 62.0 | 167.0 | 19.770038 | Kościerzyna | 4.0 | 4.0 | F |
| 54 | 54 | 20.0 | 70.0 | 131.0 | 36.334123 | Gdańsk | 4.0 | 4.0 | M |
| 56 | 56 | 62.0 | 68.0 | 147.0 | 31.500000 | Gdańsk | 3.0 | 3.0 | M |
| 59 | 59 | NaN | 35.0 | 176.0 | 10.063127 | Gdynia | 2.0 | 2.0 | F |
| 61 | 61 | NaN | 48.0 | 162.0 | 16.296923 | Gdańsk | 4.0 | 4.0 | NaN |
| 62 | 62 | NaN | 50.0 | 158.0 | 17.810845 | Gdynia | 2.0 | 0.0 | F |
| 67 | 67 | NaN | 51.0 | 175.0 | 14.872055 | Gdańsk | NaN | 0.0 | NaN |
| 68 | 68 | 37.0 | 64.0 | 153.0 | 24.311803 | Kościerzyna | 2.0 | NaN | M |
| 75 | 75 | NaN | 78.0 | 179.0 | 21.640176 | Gdańsk | 1.0 | 1.0 | NaN |
| 77 | 77 | 62.0 | 54.0 | 177.0 | 15.317326 | Gdańsk | NaN | 0.0 | NaN |
| 85 | 85 | 7.0 | 66.0 | 160.0 | 22.975990 | Kościerzyna | 3.0 | 3.0 | F |
| 93 | 93 | NaN | 55.0 | 168.0 | 17.365574 | Kościerzyna | 1.0 | 1.0 | F |
| 101 | 101 | 30.0 | 67.0 | 180.0 | 18.434224 | Gdańsk | 1.0 | 1.0 | M |
| 103 | 103 | NaN | 64.0 | 160.0 | 22.263556 | Gdańsk | 4.0 | NaN | M |
| 111 | 111 | NaN | 67.0 | 160.0 | 23.332207 | Gdańsk | 3.0 | 0.0 | M |
| 112 | 112 | 26.0 | 57.0 | 138.0 | 26.627213 | Gdynia | NaN | 0.0 | F |
| 119 | 119 | 62.0 | 62.0 | 159.0 | 24.500000 | Gdańsk | 1.0 | 1.0 | M |
| 125 | 125 | 29.0 | 66.0 | NaN | 34.700000 | Gdańsk | 4.0 | 4.0 | F |
| 128 | 128 | 58.0 | 70.0 | 168.0 | 22.085447 | Kościerzyna | NaN | 0.0 | NaN |
| 144 | 144 | 35.0 | 47.0 | 136.0 | 22.619773 | Gdańsk | 3.0 | 3.0 | M |
| 146 | 146 | NaN | 58.0 | NaN | 23.200000 | Wejherowo | 2.0 | 1.0 | F |
| 151 | 151 | NaN | 59.0 | 160.0 | 20.482471 | Gdańsk | NaN | 0.0 | M |
| 153 | 153 | 30.0 | 60.0 | 167.0 | 19.146658 | Wejherowo | 2.0 | NaN | M |
| 174 | 174 | NaN | 56.0 | 156.0 | 20.482471 | Gdańsk | NaN | 0.0 | M |
| 191 | 191 | 60.0 | 74.0 | 167.0 | 26.500000 | Kościerzyna | NaN | 0.0 | F |
| 193 | 193 | NaN | 52.0 | 152.0 | 22.500000 | Kościerzyna | 1.0 | 1.0 | M |
| 195 | 195 | 17.0 | 47.0 | 156.0 | 17.187465 | Gdańsk | NaN | 0.0 | F |
| 201 | 201 | NaN | 58.0 | 147.0 | 23.866532 | Gdańsk | 3.0 | 3.0 | M |
| 206 | 206 | 21.0 | 54.0 | 141.0 | 24.222749 | Kościerzyna | NaN | 0.0 | F |
| 214 | 214 | NaN | 81.0 | 174.0 | 23.866532 | Gdańsk | NaN | 0.0 | F |
| 217 | 217 | 17.0 | 53.0 | 175.0 | 15.406381 | Gdynia | 3.0 | 3.0 | M |
| 232 | 232 | NaN | 55.0 | 162.0 | 18.701387 | Gdańsk | 4.0 | 0.0 | M |
| 248 | 248 | 48.0 | 62.0 | 161.0 | 21.283959 | Gdynia | NaN | 0.0 | M |
| 275 | 275 | 11.0 | 54.0 | 170.0 | 16.653140 | Gdańsk | 4.0 | 4.0 | F |
| 276 | 276 | NaN | 69.0 | 163.0 | 23.154098 | Kościerzyna | 4.0 | 0.0 | M |
| 279 | 279 | NaN | 52.0 | 152.0 | 22.500000 | Kościerzyna | 3.0 | 3.0 | F |
| 283 | 283 | 7.0 | 57.0 | 144.0 | 24.489911 | Gdańsk | 4.0 | NaN | M |
| 284 | 284 | NaN | 41.0 | 168.0 | 14.500000 | Gdańsk | NaN | 0.0 | M |
| 287 | 287 | 11.0 | 49.0 | 178.0 | 15.500000 | Gdańsk | 3.0 | 3.0 | NaN |
| 289 | 289 | NaN | 54.0 | 151.0 | 21.105851 | Gdańsk | 2.0 | 2.0 | M |
| 291 | 291 | NaN | 55.0 | 160.0 | 21.500000 | Wejherowo | 2.0 | 2.0 | F |
| 295 | 295 | 47.0 | 55.0 | 168.0 | 19.500000 | Gdańsk | 1.0 | 1.0 | F |
| 109 | 109 | 17.0 | 56.0 | 184.0 | 16.500000 | Gdańsk | 4.0 | NaN | NaN |
| 157 | 157 | NaN | 78.0 | 167.0 | 24.935183 | Gdynia | 2.0 | 2.0 | F |
| 271 | 271 | 50.0 | 65.0 | 164.0 | 21.551122 | Gdynia | 2.0 | 2.0 | M |
Jak widać istnieją rekordy, dla których wartość nie zgadza się z formułą, wprowadzamy zatem poprawki:
df["bmi"] = df["weight"]/(df["height"]/100)**2
Imputacja wartości brakujących#
Rodzaje wartości brakujących
MCAR - Missing Completely At Random
MAR - Missing At Random
MNAR - Missing Not At Random
MCAR wartości brakujące powstały w sposób całkowicie losowy, co oznacza, że nie istnieje związek pomiędzy występowaniem wartości brakujących w danej zmiennej, a ich występowaniem w pozostałych zmiennych ani pomiędzy wartościami jakiejkolwiek zmiennej, a wartościami brakującymi rozważanej zmiennej.
MAR wartości brakujące występują losowo, ale można się dopatrzeć związków pomiędzy ich występowaniem, a wartościami którejś z pozostałych zmiennych.
MNAR wartości brakujące występują w sposób systematyczny, co ma związek np. ze sposobem zbierania danych, pozostałe zmienne nie mówią nic na podstawie czego można by dokonać imputacji tych wartości, natomiast prawdopodobieństwo wystąpienia braku danych jest wprost związane z wartościami omawianej zmiennej.
Na początek importujemy bibliotekę missingno, która posiada szereg przydatnych wizualizacji do zrozumienia natury wartości brakujących.
import missingno
Podstawowa wizualizacja daje intuicję na temat liczby wartości brakujących, a co więcej pokazuje też relacje pomiędzy ich występowanie w poszczególnych zmiennych.
missingno.matrix(df)
<Axes: >
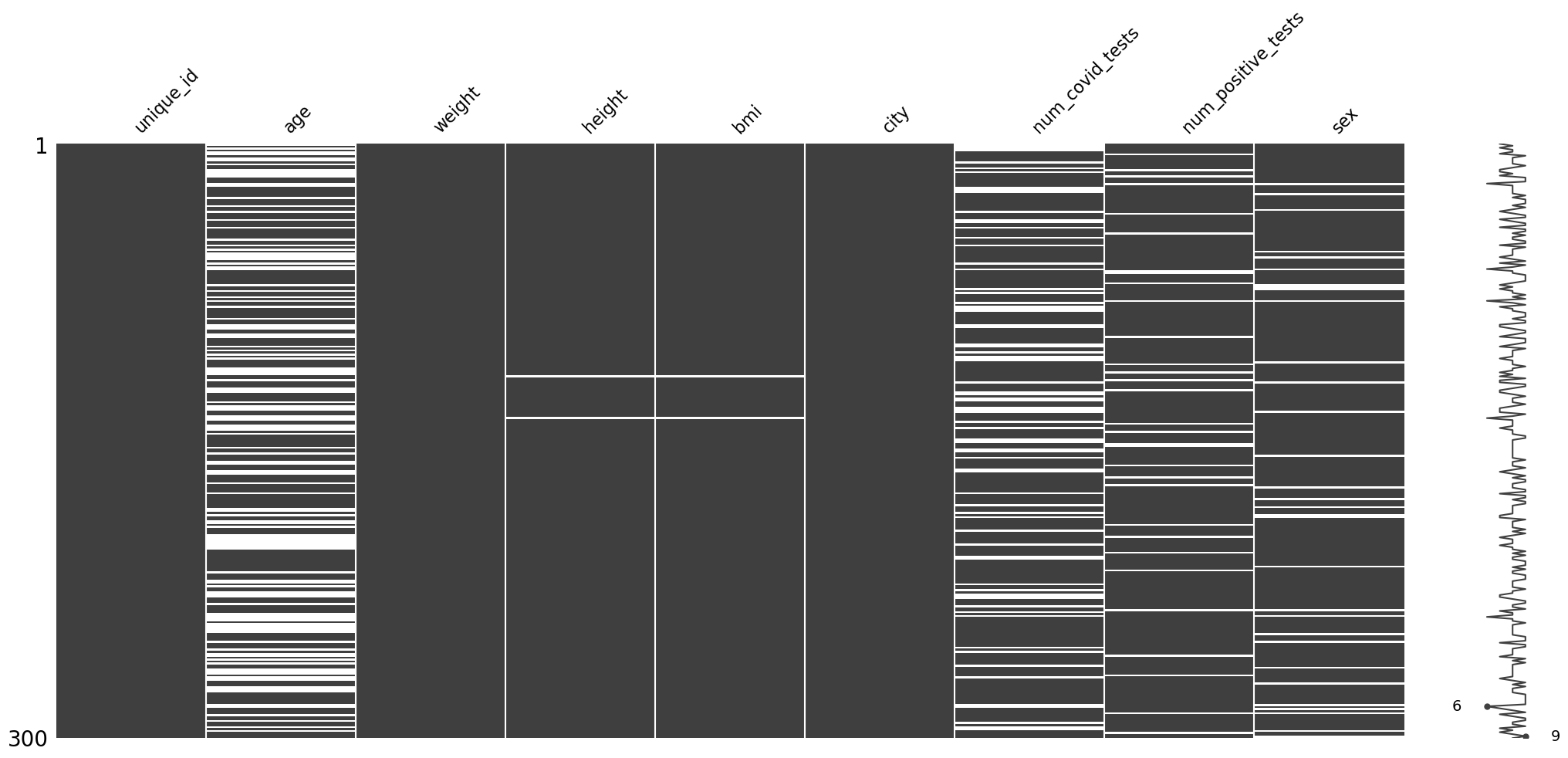
Tutaj można zauważyć relację między zmiennymi height i bmi, co jest oczywiście konsekwencją tego, że bmi jest liczone w oparciu o height. Ponadto widać też, że wartości brakujące zdecydowanie najczęściej występują dla zmiennej age.
Można również zaobserwować, że dla zmiennej age nie występują wartości wyższe niż 65 lat, zatem sposób potraktowania wartości brakujących zależy od istnienia informacji o maksymalnym wieku pacejentów w tym zbiorze danych - gdyby np okazało, że próba obejmuje również starsze osoby, ale przez jakiś błąd przy wprowadzaniu danych ich wiek się nie zapisał, należałoby potraktować taki przypadek jako MNAR i zastąpić wartością specjalną lub oznaczyć w osobnej kolumnie, w przeciwnym razie będzie to MCAR lub MAR.
Lepszemu wglądowi w to czy wartości brakujące dla danej zmiennej zależą od innych zmiennych może służyć również przedstawienie powyższej wizualizacji po posortowaniu wg wybranej zmiennej
missingno.matrix(df.sort_values("weight"))
<Axes: >
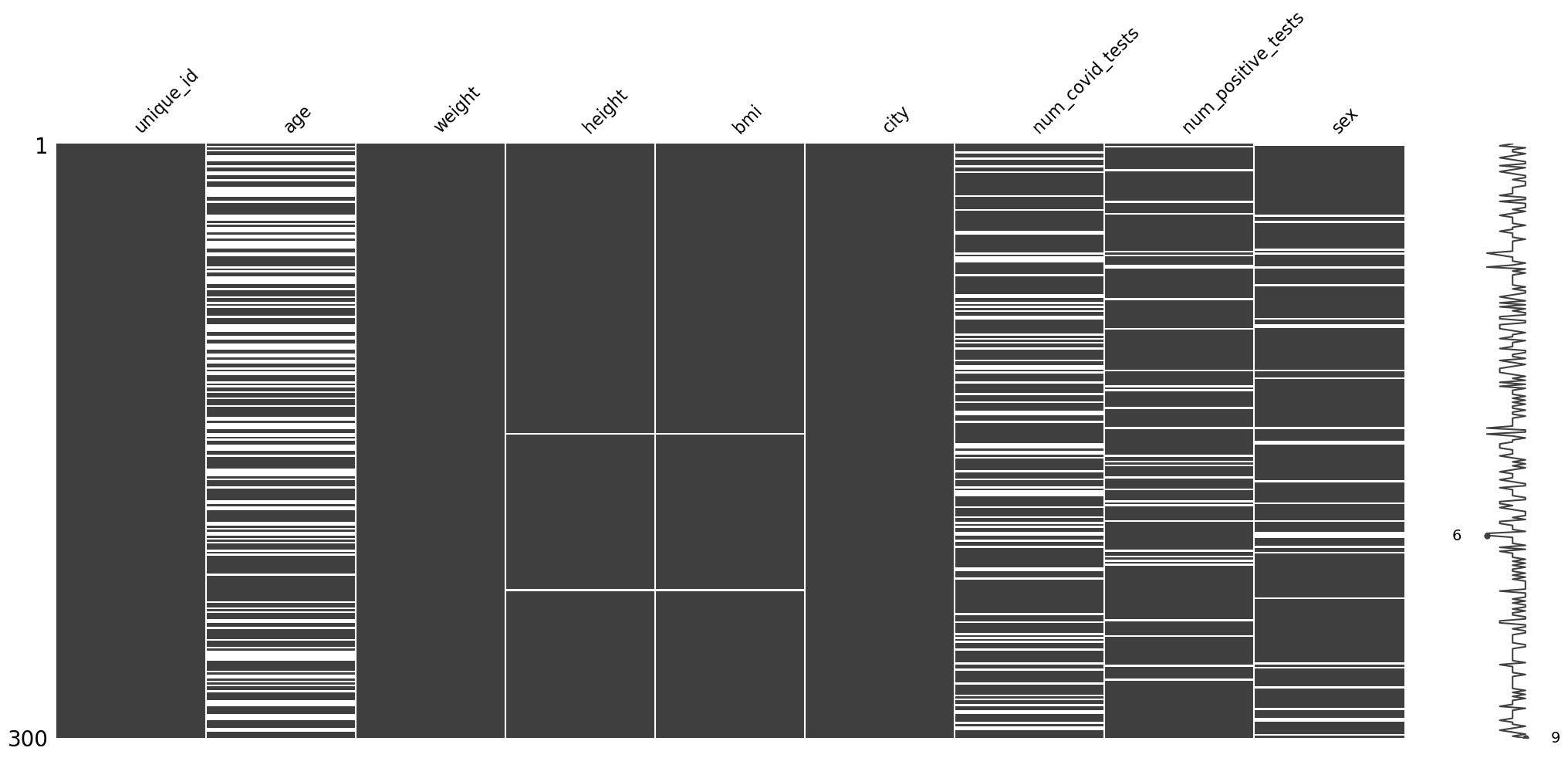
Znalezieniu relacji może służyć również heatmap macierzy korelacji.
missingno.heatmap(df, cmap='rainbow')
<Axes: >
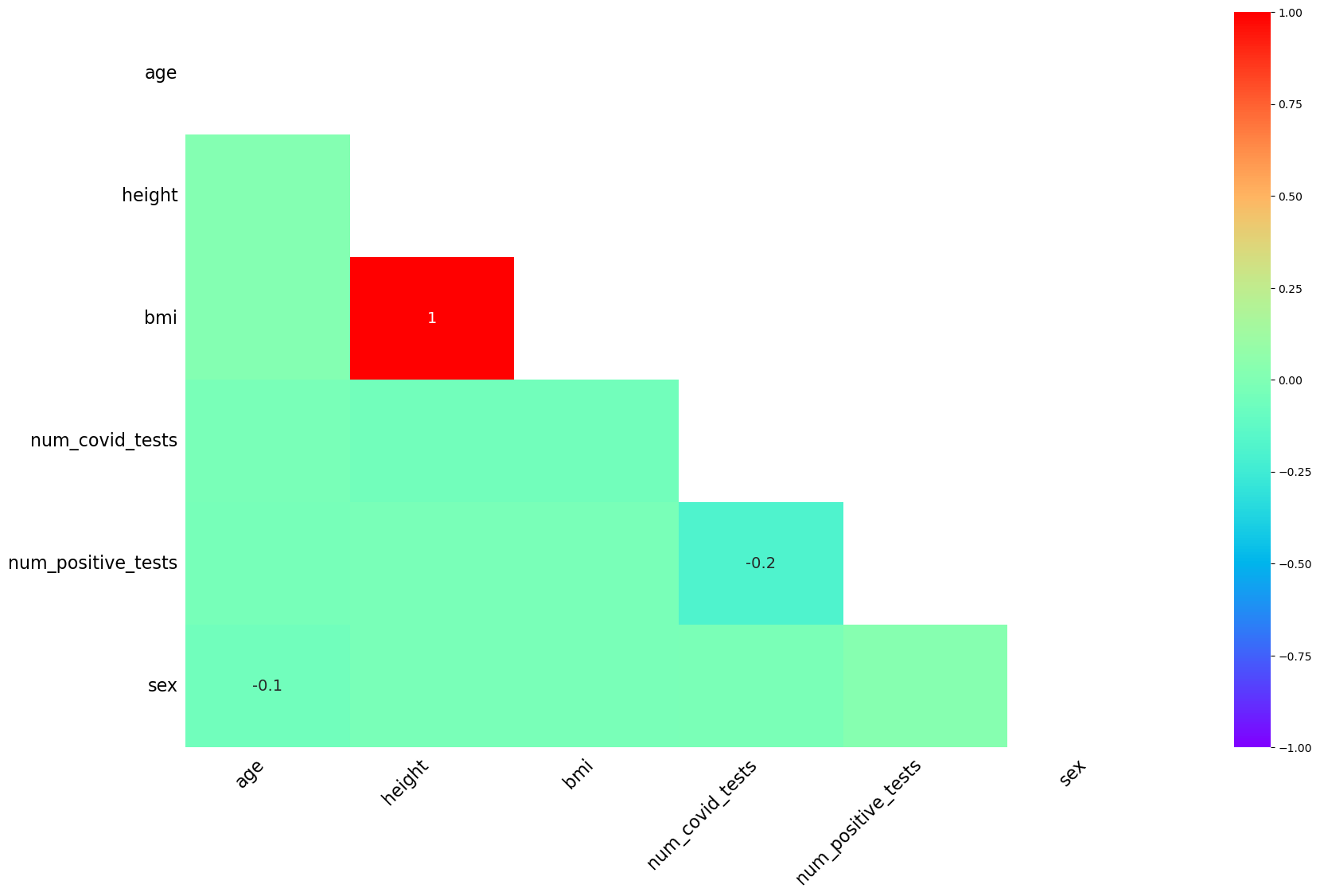
Przyjmijmy, że faktycznie wystąpił systematyczny błąd przy zapisywaniu zmiennej age zatem reprezentuje ona MNAR, zmienna bmi w oczywisty sposób będzie MAR jako, że odwołuje się teraz wprost do innej zmiennej, pozostałe zmienne jeśli nie mamy jakiejś dodatkowej informacji co do natury powstania wartości brakujących należy uznać za MCAR
Metody imputacji brakujących wartości#
Wszystkie przekształcenia wykorzystujące informacje o rozkładach cech należy implementować najpierw na zbiorze treningowym, a następnie w oparciu o rozkład ze zbioru treningowego - na zbiorze testowym. Inaczej wykorzystujemy informacje ze zbioru testowego i przestaje on być niezależny.
każdej brakującej obserwacji danej zmiennej przypisujemy np -1, -999 lub “N/A”, świadomie stosując wartość niewystępującą w obserwacjach bez brakującej wartości
przede wszystkim dla typu MNAR, gdzie zazwyczaj jest to jedyne prawidłowe podejście
można zastosować tutaj również 0 jeśli w naturalny sposób oznacza ono brak danego zjawiska i logika biznesowa nakazuje tak interpretować wartość brakującą
każdej brakującej obserwacji danej zmiennej przypisujemy tę samą wartość, w odróżnieniu od poprzedniej metody jest ona wyliczona w oparciu o dane treningowe
imputacja średnią - zachowuje średnią z danych, ale zaniża wariancję, może być narażona na wpływ wartości odstających
imputacja medianą - wolna od wpływu wartości odstających, ale wpływa na średnią i wariancję
imputacja modą - najczęściej stosowana dla zmiennych kategorycznych, jeśli nie mają charakteru MNAR
podobna do opisanej wyżej imputacji wartością stałą lecz realizowana osobno dla każdej zdefiniowanej w danych grupy
to jak dobrać grupy może wynikać z wiedzy biznesowej lub z EDA
w odróżnieniu od omówienych wcześniej metod, nie używamy tu tej samej wartości do wypełniania wszystkich obserwacji
może polegać na losowaniu wartości spośród niepustych obserwacji danej zmiennej lub dopasowaniu do niej rozkładu statystycznego i losowaniu z rozkładu
do stosowania w szeregach czasowych
może obejmować zastąpienie brakujących obserwacji za pomocą poprzedniej wartości lub kolejnej wartości
można stosować również metody oparte o większą liczbę poprzednich obserwacji np średnia krocząca
dobrze może się sprawdzać również interpolacja
Imputacja z wykorzystaniem modelu
obejmuje przewidywanie brakujących wartości zmiennej na podstawie pozostałych zmiennych lub ich podgrupy
stosowane są tu zarówno algorytmy regresji jak i KNN lub modele drzewiaste
Przykłady imputacji#
Imputacja wartością specjalną#
Zmienną age uznaliśmy za MNAR, co sugeruje, że nie można się posłużyć statystykami z próbki, tylko należy użyć wartości specjalnej. Jeśli wiemy, że wartości brakujące reprezentują starsze osoby wstawienie tutaj wartości np. -1 może nie być najlepszym rozwiązaniem, ponieważ takie podejście może zaburzyć monotoniczność relacji tej zmiennej ze zmienną celu, zamiast tego można spróbować wartości większej niż maksimum z obecnych danych np 70
df["age"] = df["age"] .fillna(70)
df.info()
<class 'pandas.core.frame.DataFrame'>
Index: 300 entries, 0 to 209
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 300 non-null int64
1 age 300 non-null float64
2 weight 300 non-null float64
3 height 298 non-null float64
4 bmi 298 non-null float64
5 city 300 non-null object
6 num_covid_tests 226 non-null float64
7 num_positive_tests 269 non-null float64
8 sex 269 non-null object
dtypes: float64(6), int64(1), object(2)
memory usage: 23.4+ KB
Imputacja wartością stałą#
Pozostałe zmienne z brakującymi wartościami należy wypełnić w oparciu o wartości z danych treningowych, zanim do tego przystąpimy należy podzielić próbkę, co będzie reprezentowało rzeczywistą sytuację, gdy na podstawie dostępnych danych będziemy uzupełniać te przyszłe.
from sklearn.model_selection import train_test_split
X_train, X_test = train_test_split(df, test_size =0.25, random_state=42)
Tutaj dla uproszczenia stosujemy tylko prosty podział na zbiór treningowy i testowy, generalnie najlepszą praktyką jest wydzielenie osobnego zbioru testowego reprezentującego zdolność modelu do generalizacji na nowych, niewidzianych wcześniej danych i dobór najlepszego zestawu parametrów i transformacji stosując crosswalidację na zbiorze treningowym.
Imputacja zmiennych kategorycznych#
W przypadku zmiennych kategorycznych, gdy nie stosujemy imputacji wartością specjalną najczęściej spotykaną strategią jest wypełnianie najczęściej występującą wartością w danych treningowych.
X_train_sex_mode = X_train["sex"].dropna().mode()[0]
X_train["sex"] = X_train["sex"].fillna(X_train_sex_mode)
X_test["sex"] = X_test["sex"].fillna(X_train_sex_mode)
Alternatywnie można też skorzystać z klasy SimpleImputer z biblioteki sklearn. Użycie tego typu transformerów stanowi dobrą praktykę, ponieważ można je potem łączyć w pipeline co ułatwia development i zmniejsza ryzyko popełnienia błędów takich jak np. data leakage. Poniżej zaprezentujemy ponowny podział na zbiór treningowy i testowy oraz wypełnienie tej samej zmiennej z użyciem klasy SimpleImputer.
from sklearn.impute import SimpleImputer
X_train, X_test = train_test_split(df, test_size =0.25, random_state=42)
si_mode = SimpleImputer(strategy="most_frequent")
si_mode.fit(X_train["sex"].values.reshape(-1, 1))
X_train["sex"] = si_mode.transform(X_train["sex"].values.reshape(-1, 1)).reshape(-1)
X_test["sex"] = si_mode.transform(X_test["sex"].values.reshape(-1, 1)).reshape(-1)
X_train.info()
<class 'pandas.core.frame.DataFrame'>
Index: 225 entries, 297 to 108
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 225 non-null int64
1 age 225 non-null float64
2 weight 225 non-null float64
3 height 223 non-null float64
4 bmi 223 non-null float64
5 city 225 non-null object
6 num_covid_tests 173 non-null float64
7 num_positive_tests 203 non-null float64
8 sex 225 non-null object
dtypes: float64(6), int64(1), object(2)
memory usage: 17.6+ KB
Powyżej stosujemy SimpleImputer na tylko jednej kolumnie, inaczej wszystkie zmienne z brakującymi wartościami zostałyby wypełnione swoją najczęstszą wartością. Standardową praktyką jest użycie klasy ColumnTransformer do przypisywania odpowiednich transformacji poszczególnym grupom zmiennych, co zostanie zaprezentowane później.
Imputacja zmiennych numerycznych#
Załóżmy, że chcemy zainputować zmienne numeryczne korzystając z mediany, użycie mediany może być dobrą alternatywą dla używania średniej jeśli obawiamy się wpływu wartości odstających na średnią.
si_median = SimpleImputer(strategy="median")
X_train_num = X_train.select_dtypes(exclude="object")
X_test_num = X_test.select_dtypes(exclude="object")
si_median.fit(X_train_num)
X_train_num = pd.DataFrame(si_median.transform(X_train_num), columns =X_train_num.columns)
X_test_num = pd.DataFrame(si_median.transform(X_test_num), columns =X_test_num.columns)
X_train = pd.concat([X_train_num, X_train.select_dtypes(include="object")],axis=1)
X_test = pd.concat([X_test_num, X_test.select_dtypes(include="object")],axis=1)
X_train.info()
<class 'pandas.core.frame.DataFrame'>
Index: 280 entries, 0 to 285
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 225 non-null float64
1 age 225 non-null float64
2 weight 225 non-null float64
3 height 225 non-null float64
4 bmi 225 non-null float64
5 num_covid_tests 225 non-null float64
6 num_positive_tests 225 non-null float64
7 city 225 non-null object
8 sex 225 non-null object
dtypes: float64(7), object(2)
memory usage: 21.9+ KB
Łączenie różnych metod imputacji z wykorzystaniem pipeline#
Jak już wspomniano najlepszą praktykę przy stosowaniu imputacji stanowi łączenie poszczególnych transformacji w Pipeline będący ciągiem transformacji, który może też na końcu zawierać model predykcyjny. Tutaj pokażemy pipeline łączący wszystkie wcześniej stosowane operacje imputacji danych.
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
# przywrócenie danych do postaci sprzed imputacji
df["age"] = np.where(df["age"]>65, np.nan, df["age"])
X_train, X_test = train_test_split(df, test_size =0.25, random_state=42)
columns_to_impute_special_value =["age"]
columns_to_impute_mode = X_train.select_dtypes(include="object").columns.tolist()
columns_to_impute_median = list(set(X_train.select_dtypes(exclude="object").columns.tolist()) -set(columns_to_impute_special_value))
pipeline_sv = Pipeline(steps=[("special_value_imputer", SimpleImputer(strategy="constant", fill_value=70))])
pipeline_mode = Pipeline(steps=[("mode_imputer",SimpleImputer(strategy="most_frequent"))])
pipeline_num = Pipeline(steps=[("median_imputer",SimpleImputer(strategy="median"))])
column_transformer = ColumnTransformer(
transformers=[
('special_value_imputation', pipeline_sv, columns_to_impute_special_value),
('mode_imputation', pipeline_mode, columns_to_impute_mode),
('median_imputation', pipeline_num, columns_to_impute_median)
])
imputation_pipeline = Pipeline(steps=[("imputation", column_transformer)])
imputation_pipeline.fit(X_train)
X_train = pd.DataFrame(imputation_pipeline.transform(X_train), columns=X_train.columns)
X_test = pd.DataFrame(imputation_pipeline.transform(X_test), columns=X_test.columns)
X_test.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 75 entries, 0 to 74
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 75 non-null object
1 age 75 non-null object
2 weight 75 non-null object
3 height 75 non-null object
4 bmi 75 non-null object
5 city 75 non-null object
6 num_covid_tests 75 non-null object
7 num_positive_tests 75 non-null object
8 sex 75 non-null object
dtypes: object(9)
memory usage: 5.4+ KB
Imputacja wg grupy#
Wróćmy na chwilę do zmiennej age, załóżmy, że jej braki danych nie są jednak wynikiem systematycznego błędu lecz występują losowo, a co więcej wiemy, że każde z miast ze zmiennej city charakteryzuje się specyficznym rozkładem dla zmiennej age. Wówczas imputacja mogłaby tutaj wyglądać następująco
X_train, X_test = train_test_split(df, test_size =0.25, random_state=42)
mean_age_by_city =X_train.groupby("city")["age"].mean().reset_index()
X_train = X_train.merge(mean_age_by_city, on ="city",suffixes=("","_mean"))
X_test = X_test.merge(mean_age_by_city, on ="city",suffixes=("","_mean"))
X_train["age"] = X_train["age"].fillna(X_train["age_mean"])
X_test["age"] = X_test["age"].fillna(X_test["age_mean"])
X_train.drop("age_mean", axis=1, inplace=True)
X_test.drop("age_mean", axis=1, inplace=True)
X_test.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 75 entries, 0 to 74
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 75 non-null int64
1 age 75 non-null float64
2 weight 75 non-null float64
3 height 75 non-null float64
4 bmi 75 non-null float64
5 city 75 non-null object
6 num_covid_tests 53 non-null float64
7 num_positive_tests 66 non-null float64
8 sex 67 non-null object
dtypes: float64(6), int64(1), object(2)
memory usage: 5.4+ KB
Imputacja z wykorzystaniem modelu#
Poniżej pokażemy jeszcze jak można do imputacji wykorzystać model ML na przykładzie klasy KNNImputer, która wykonuje imputację na podstawie wartości najbliższych obserwacji.
from sklearn.impute import KNNImputer
X_train, X_test = train_test_split(df, test_size =0.25, random_state=42)
X_train_num = X_train.select_dtypes(exclude="object")
X_test_num = X_test.select_dtypes(exclude="object")
knn = KNNImputer(n_neighbors=5)
knn.fit(X_train_num)
X_train_num = pd.DataFrame(knn.transform(X_train_num), columns= X_train_num.columns)
X_test_num = pd.DataFrame(knn.transform(X_test_num), columns= X_test_num.columns)
X_train = pd.concat([X_train_num, X_train.select_dtypes(include="object")],axis=1)
X_test = pd.concat([X_test_num, X_test.select_dtypes(include="object")],axis=1)
X_train.info()
<class 'pandas.core.frame.DataFrame'>
Index: 280 entries, 0 to 285
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 225 non-null float64
1 age 225 non-null float64
2 weight 225 non-null float64
3 height 225 non-null float64
4 bmi 225 non-null float64
5 num_covid_tests 225 non-null float64
6 num_positive_tests 225 non-null float64
7 city 225 non-null object
8 sex 202 non-null object
dtypes: float64(7), object(2)
memory usage: 21.9+ KB
Metody usuwania brakujących wartości#
Drugim oprócz imputacji sposobem radzenia sobie z wartościami brakującymi jest ich usuwanie. Wybór pomiędzy usuwaniem, a imputacją zależy w dużym stopniu od ilości dostępnych danych oraz poziomu koncentracji wartości brakujących, a także tego jak istotne są dla nas dane zmienne lub obserwacje.
Należy pamiętać, żeby w przypadku stosowania usuwania brakujących obserwacji zacząć od usunięcia wszystkich niepotrzebnych kolumn, ponieważ mogą one potem niepotrzebnie wpłynąć na usuwanie obserwacji.
Najwygodniejszą opcją usuwania w bibliotece pandas jest funkcja dropna, kilka przykładów poniżej
# usuwanie wszystkich obserwacji z jakimikolwiek wartościami brakującymi
df_nonull = df.dropna(axis=0, how="any")
df_nonull.info()
<class 'pandas.core.frame.DataFrame'>
Index: 97 entries, 6 to 49
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 97 non-null int64
1 age 97 non-null float64
2 weight 97 non-null float64
3 height 97 non-null float64
4 bmi 97 non-null float64
5 city 97 non-null object
6 num_covid_tests 97 non-null float64
7 num_positive_tests 97 non-null float64
8 sex 97 non-null object
dtypes: float64(6), int64(1), object(2)
memory usage: 7.6+ KB
# usuwanie wszystkich obserwacji z progiem co najmniej 2 wartości brakujących
df_nonull = df.dropna(axis=0, thresh=df.shape[1]-2)
df_nonull.info()
<class 'pandas.core.frame.DataFrame'>
Index: 294 entries, 0 to 209
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 294 non-null int64
1 age 179 non-null float64
2 weight 294 non-null float64
3 height 293 non-null float64
4 bmi 293 non-null float64
5 city 294 non-null object
6 num_covid_tests 223 non-null float64
7 num_positive_tests 265 non-null float64
8 sex 268 non-null object
dtypes: float64(6), int64(1), object(2)
memory usage: 23.0+ KB
# usuwanie wszystkich obserwacji z progiem co najmniej 1 wartością brakującą dla kolumn age, num_covid_tests i num_positive_tests
df_nonull = df.dropna(axis=0, thresh=2, subset=["age", "num_covid_tests", "num_positive_tests"])
df_nonull.info()
<class 'pandas.core.frame.DataFrame'>
Index: 261 entries, 1 to 209
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 261 non-null int64
1 age 179 non-null float64
2 weight 261 non-null float64
3 height 259 non-null float64
4 bmi 259 non-null float64
5 city 261 non-null object
6 num_covid_tests 215 non-null float64
7 num_positive_tests 241 non-null float64
8 sex 235 non-null object
dtypes: float64(6), int64(1), object(2)
memory usage: 20.4+ KB
# usuwanie kolumn mających co najmniej 10% wartości brakujących
df_nonull = df.dropna(axis=1, thresh=0.9*df.shape[0])
df_nonull.info()
<class 'pandas.core.frame.DataFrame'>
Index: 300 entries, 0 to 209
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 unique_id 300 non-null int64
1 weight 300 non-null float64
2 height 298 non-null float64
3 bmi 298 non-null float64
4 city 300 non-null object
dtypes: float64(3), int64(1), object(1)
memory usage: 14.1+ KB
Czyszczenie szeregów czasowych#
df_ts = generate_ts_data()
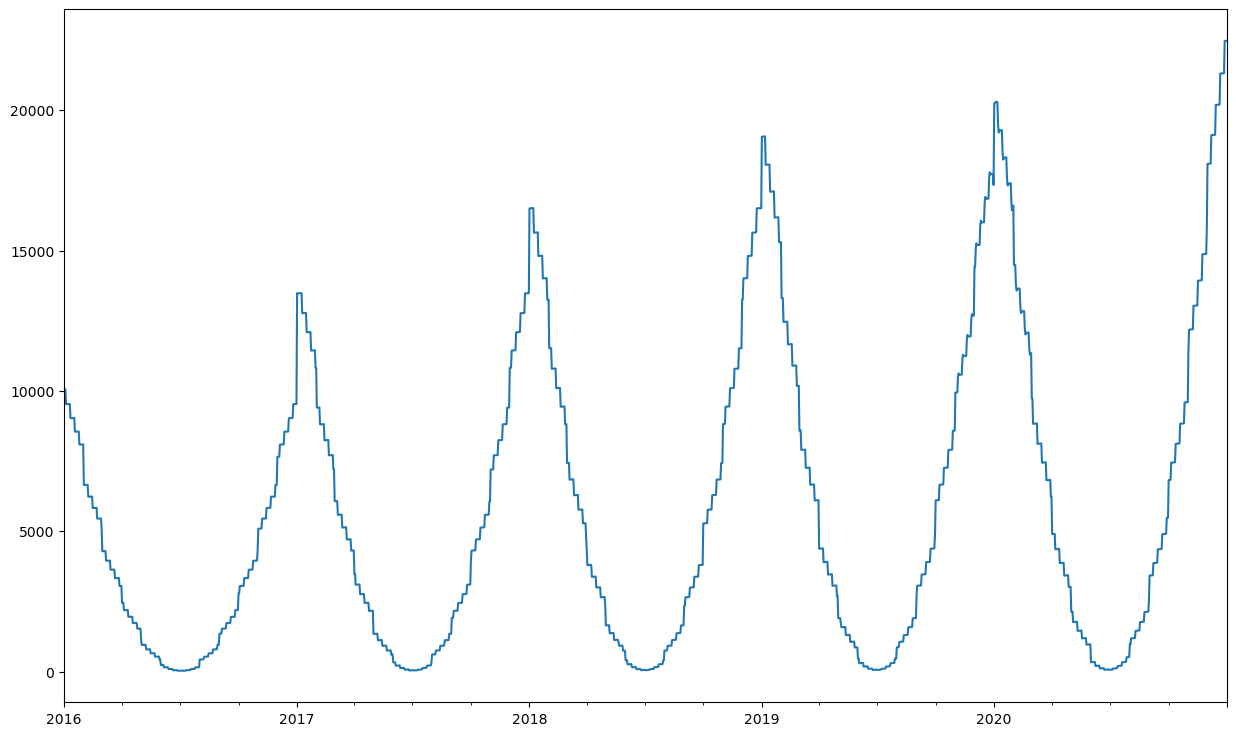
df_ts.set_index("SalesDate").plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
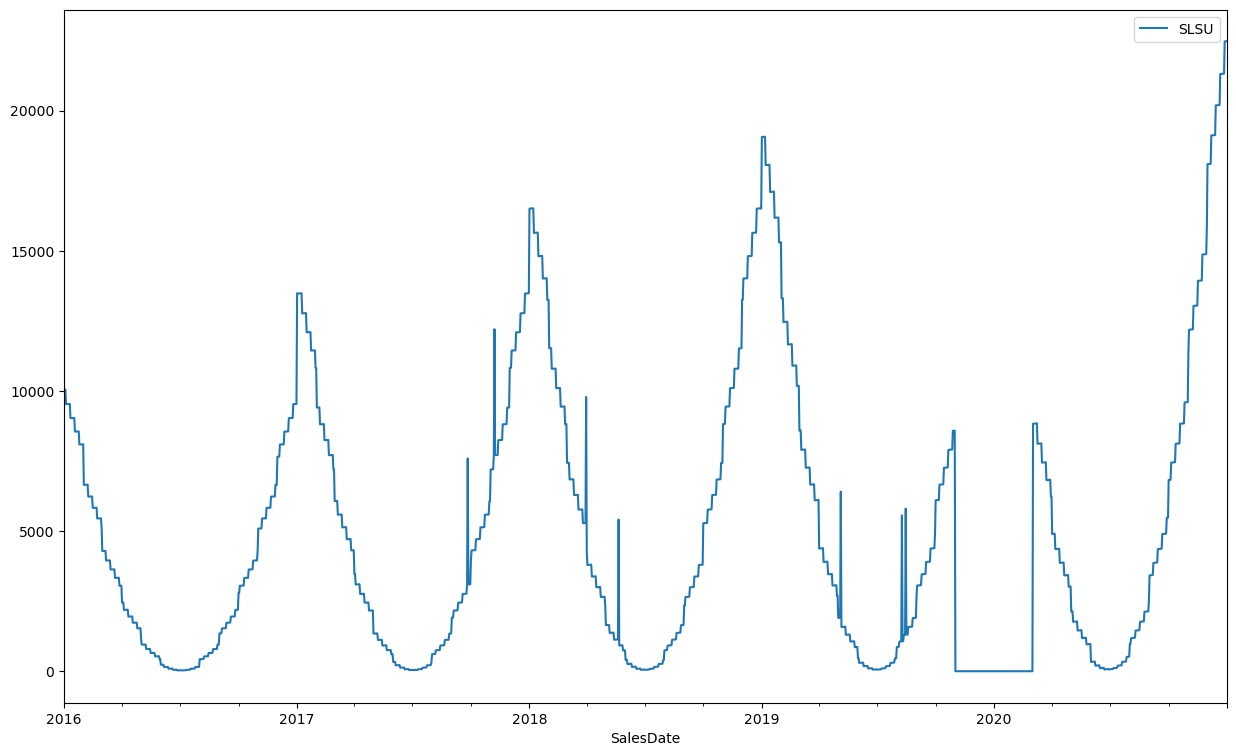
W czyszczeniu danych o charakterze szeregu czasowego bardzo użyteczna jest wizualna analiza danych. Analizując powyższy wykres można dostrzec dość regularny szereg czasowy z rocznym okresem sezonowości i trendem rosnącym. Widać również zaburzenia w postaci nieregularnie rozlokowanych pików w pojedynczych dniach oraz silnie zaburzony okres na przełomie 2019 i 2020.
df_ts.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1827 entries, 0 to 1826
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 SalesDate 1827 non-null datetime64[ns]
1 SLSU 1827 non-null float64
dtypes: datetime64[ns](1), float64(1)
memory usage: 28.7 KB
Przed przejściem do dalszej analizy należy jeszcze upewnić się, że dane mają prawidłowe formaty i są odpowiednio posortowane, inaczej łatwo o błędne wnioski.
df_ts["SLSU"] = df_ts["SLSU"].astype("float64")
df_ts.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1827 entries, 0 to 1826
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 SalesDate 1827 non-null datetime64[ns]
1 SLSU 1827 non-null float64
dtypes: datetime64[ns](1), float64(1)
memory usage: 28.7 KB
df_ts = df_ts.sort_values("SalesDate")
df_ts = df_ts.set_index("SalesDate")
df_ts.plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>

df_ts.index.nunique(), df_ts.shape[0]
(1827, 1827)
Dane nie mają duplikatów, są posortowane a formaty są już poprawne, możemy się zatem skupić na oznaczaniu i imputacji wartości zaburzonych.
Podstawą do oznaczenia danego zjawiska jako zaburzonego, a następnie jego imputacji powinna być zawsze wiedza biznesowa odnośnie tego czy dane zjawisko ma charakter jednorazowy i już się nie powtórzy w analogicznym okresie.
Istnieje wiele metod oznaczania anomalii w szeregach czasowych, mogą one też być mocno zależne od wiedzy na tematy powodu wystąpienia takiej anomali. Tutaj najpierw spróbujemy automatycznie wykryć pojedyncze zaburzenia w oparciu o porównanie z medianą z sąsiednich obserwacji.
df_ts["moving_SLSU_median_3"] = df_ts["SLSU"].rolling(3, center=True, min_periods=1).median()
df_ts.plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
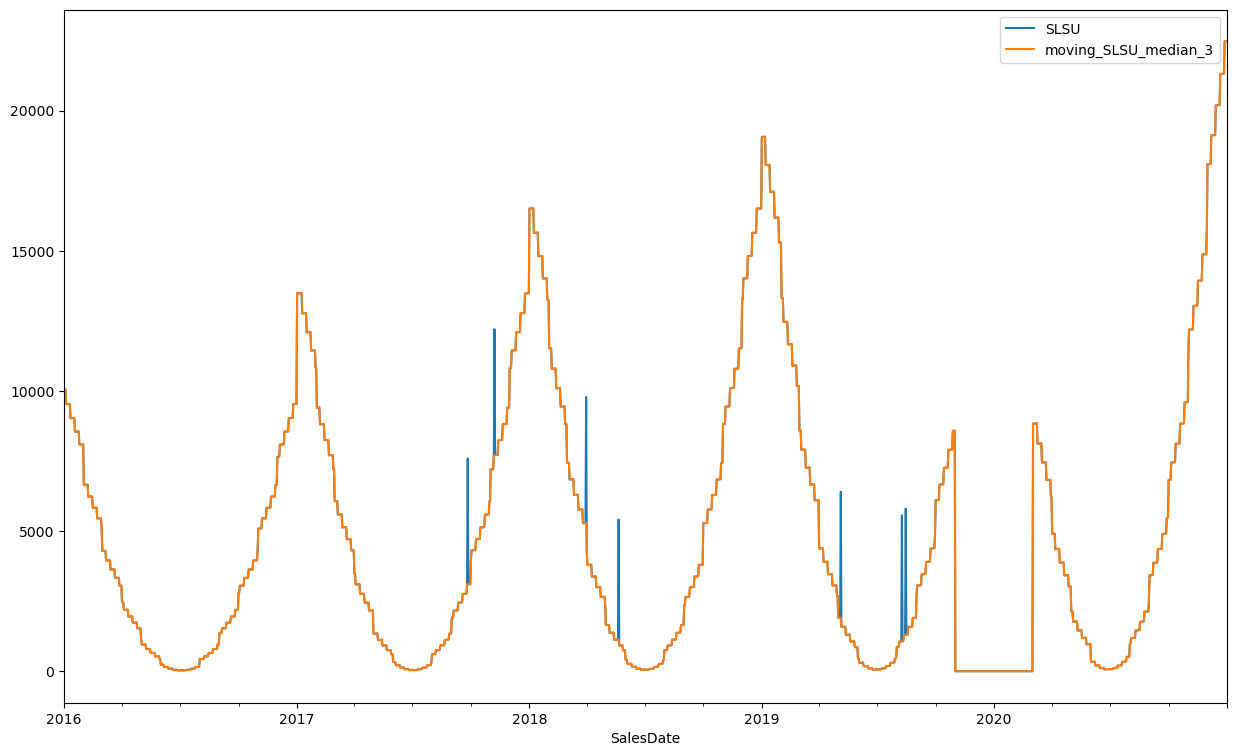
jak widać takie podejście dobrze oddziela naturalne obserwacje od pojedynczych zaburzeń, można za jego pomocą oznaczyć wartości odstające jeśli np zauważymy, że różnica pomiędzy wyliczoną medianą a wartością pierwotną wynosi ponad 15%
len(df_ts.loc[np.abs(df_ts["moving_SLSU_median_3"]-df_ts["SLSU"])>0.15*df_ts["SLSU"] ])
7
df_ts["SLSU"] =np.where(np.abs(df_ts["moving_SLSU_median_3"]-df_ts["SLSU"])>0.15*df_ts["SLSU"], np.nan, df_ts["SLSU"])
df_ts["SLSU"].plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
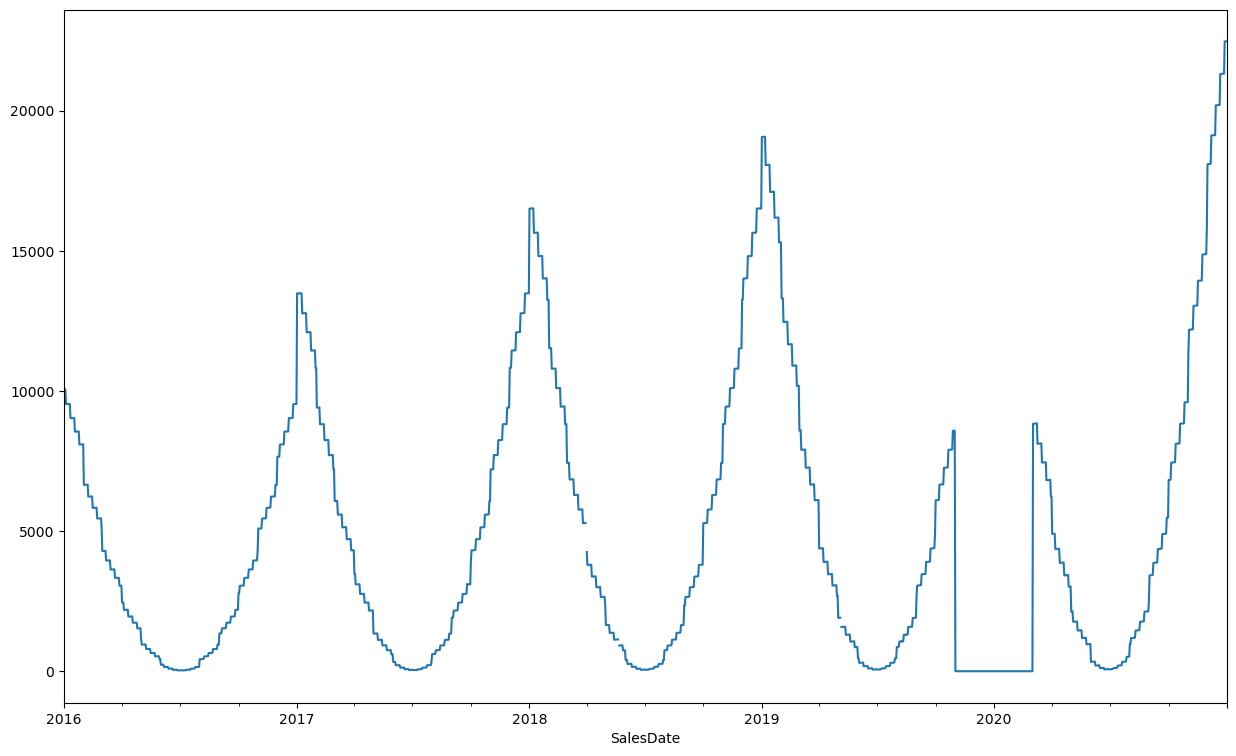
Należy mieć świadomość, że przedstawiona powyżej metoda może również oznaczyć jako anomalia zupełnie naturalnie występujące obserwacje, wszystko zależy od konkretnej potrzeby przy czyszczeniu szeregu czasowego.
Obserwacje oznaczone jako puste można następnie zaimputować za pomocą wyliczonej wcześniej mediany lub dokonać interpolacji liniowej
df_ts["SLSU"] = df_ts["SLSU"].interpolate(method="linear")
df_ts["SLSU"].plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
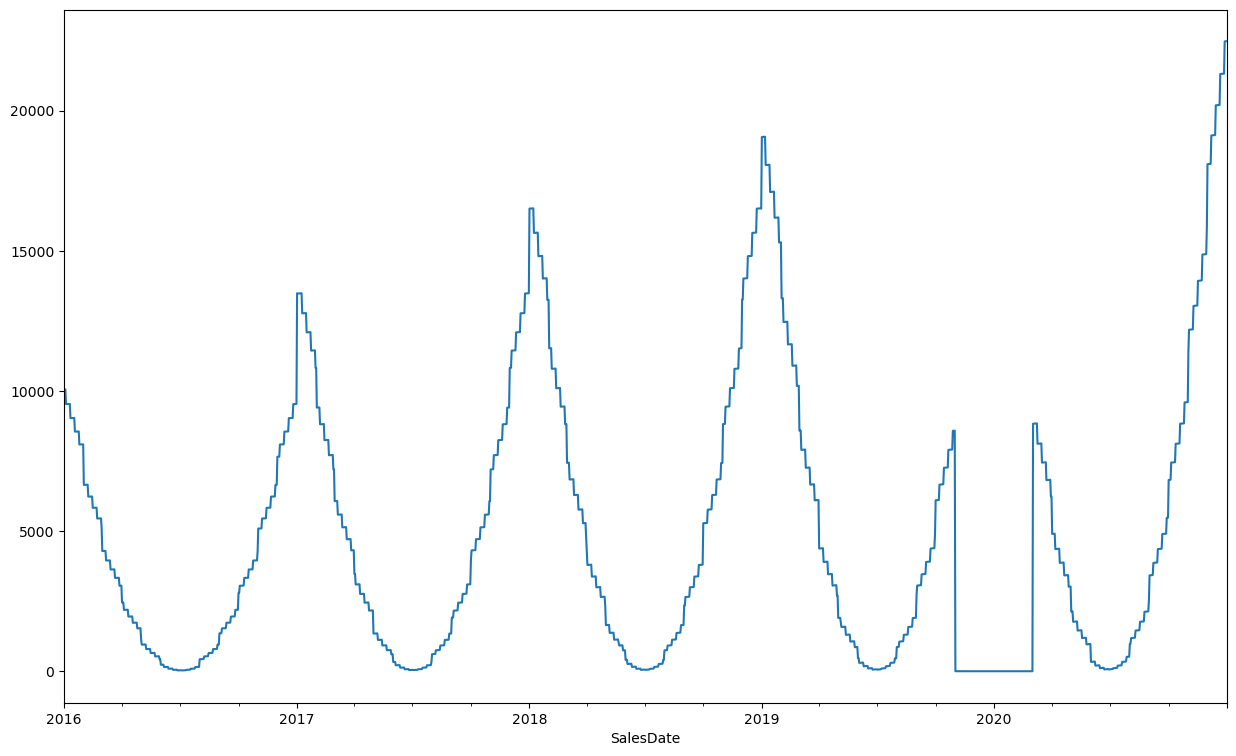
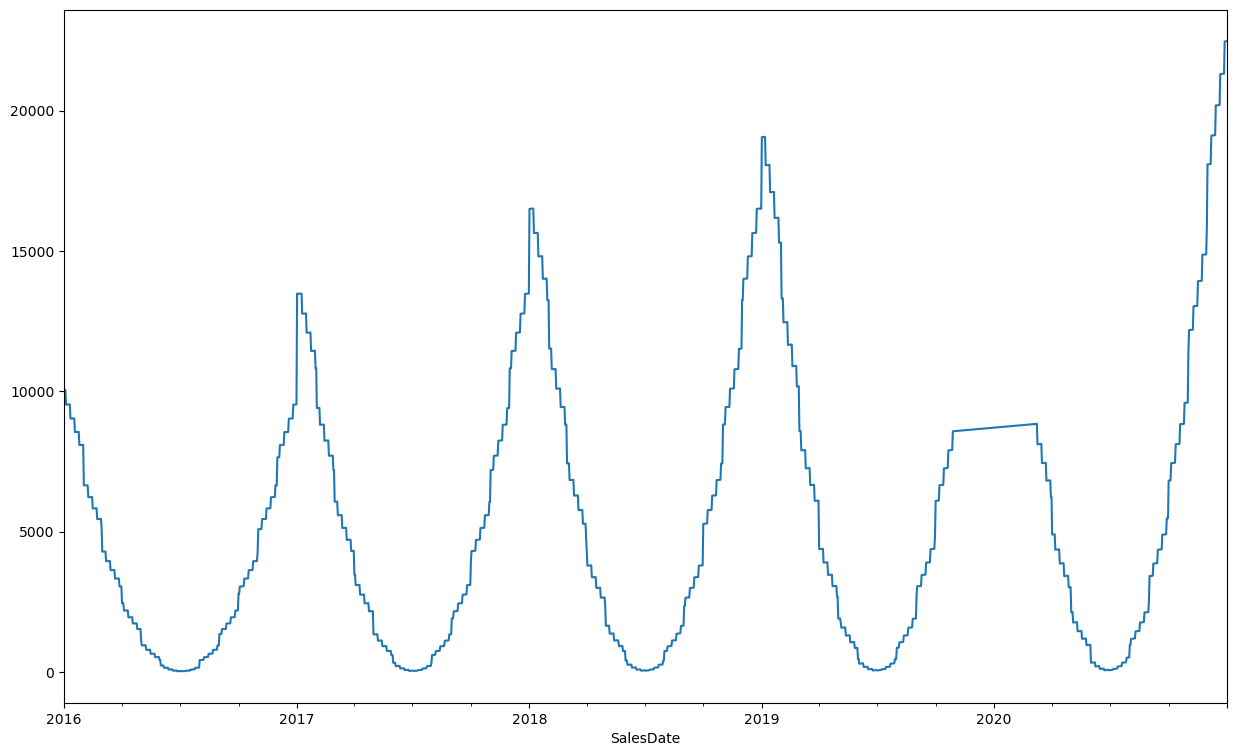
Jak widać z poniższego wykresu, interpolacja liniowa nie będzie jednak użyteczna w celu wypełnienia dłuższych zaburzeń, w szczególności w przypadku gdy przypadają one w okresie sezonowego szczytu. Zamiast tego spróbujmy dokonać prognozy modelem szeregu czasowego w oparciu o wcześniejsze, niezaburzone dane.
df_ts["SLSU"] = np.where(df_ts["SLSU"]==0, np.nan, df_ts["SLSU"])
df_ts["SLSU"].interpolate(method="linear").plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
df_ts["SLSU"] = df_ts["SLSU"].fillna(0)
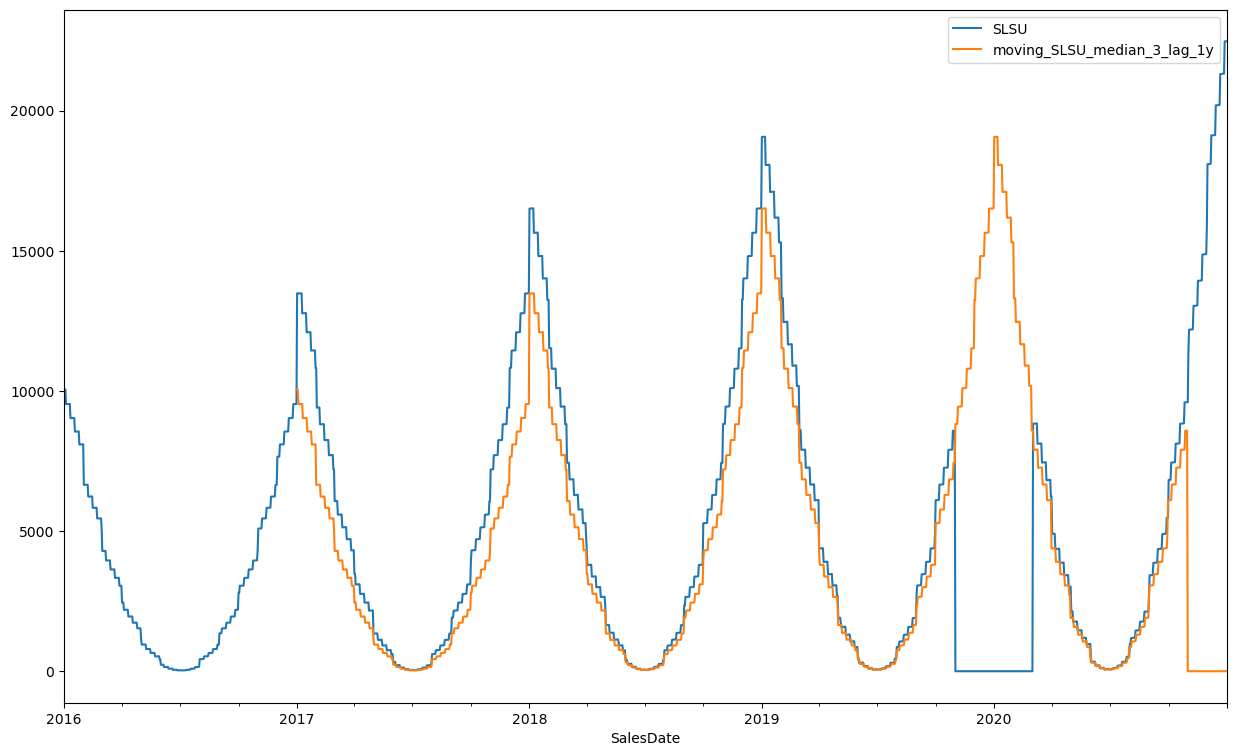
Automatycznym sposobem na oznaczenie wartości odstających przy założeniu, że nie można tutaj po prostu patrzeć na obserwacje z wartością 0 jest porównanie z wartością sprzed roku a jeszcze lepiej z wygładzoną wartością, więc wygodnie jest użyć wyliczonej już wcześniej mediany kroczącej sprzed roku.
df_ts["moving_SLSU_median_3_lag_1y"] = df_ts["moving_SLSU_median_3"].shift(365)
df_ts[["SLSU", "moving_SLSU_median_3_lag_1y"]].plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
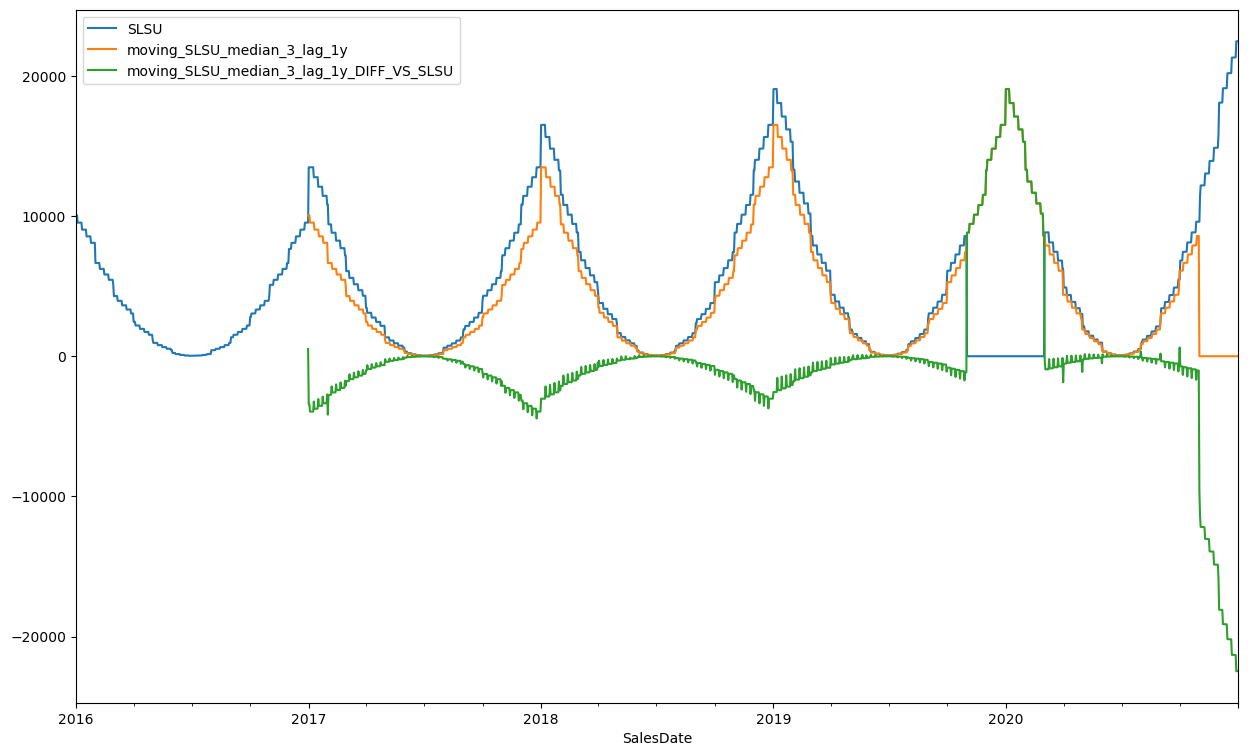
Następnie można wyliczyć różnice pomiędzy wartością SLSU, a medianą i oznaczyć jako puste wartości odstające wyznaczone np metodą IQR, przyjmując dodatkowo warunek, że interesują nas tylko wartości większe od IQR, aby nie wyzerować wartości rok po zaburzeniu.
df_ts["moving_SLSU_median_3_lag_1y_DIFF_VS_SLSU"] =df_ts["moving_SLSU_median_3_lag_1y"] - df_ts["SLSU"]
df_ts[["SLSU", "moving_SLSU_median_3_lag_1y", "moving_SLSU_median_3_lag_1y_DIFF_VS_SLSU"]].plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
df_ts["IQR"] = (df_ts["moving_SLSU_median_3_lag_1y_DIFF_VS_SLSU"].quantile(0.75) - df_ts["moving_SLSU_median_3_lag_1y_DIFF_VS_SLSU"].quantile(0.25))*1.5
df_ts.loc[df_ts["moving_SLSU_median_3_lag_1y_DIFF_VS_SLSU"] >df_ts["IQR"] ]
| SLSU | moving_SLSU_median_3 | moving_SLSU_median_3_lag_1y | moving_SLSU_median_3_lag_1y_DIFF_VS_SLSU | IQR | |
|---|---|---|---|---|---|
| SalesDate | |||||
| 2019-11-01 | 0.0 | 0.0 | 8818.736687 | 8818.736687 | 2249.224099 |
| 2019-11-02 | 0.0 | 0.0 | 8820.468738 | 8820.468738 | 2249.224099 |
| 2019-11-03 | 0.0 | 0.0 | 8822.200788 | 8822.200788 | 2249.224099 |
| 2019-11-04 | 0.0 | 0.0 | 8823.932839 | 8823.932839 | 2249.224099 |
| 2019-11-05 | 0.0 | 0.0 | 9437.078825 | 9437.078825 | 2249.224099 |
| ... | ... | ... | ... | ... | ... |
| 2020-02-26 | 0.0 | 0.0 | 10179.000000 | 10179.000000 | 2249.224099 |
| 2020-02-27 | 0.0 | 0.0 | 10181.000000 | 10181.000000 | 2249.224099 |
| 2020-02-28 | 0.0 | 0.0 | 10181.000000 | 10181.000000 | 2249.224099 |
| 2020-02-29 | 0.0 | 0.0 | 8587.000000 | 8587.000000 | 2249.224099 |
| 2020-03-01 | 0.0 | 0.0 | 8587.000000 | 8587.000000 | 2249.224099 |
122 rows × 5 columns
df_ts["SLSU"] = np.where(df_ts["moving_SLSU_median_3_lag_1y_DIFF_VS_SLSU"] >df_ts["IQR"],np.nan, df_ts["SLSU"])
df_ts["SLSU"].plot(figsize=(15,9))
<Axes: xlabel='SalesDate'>
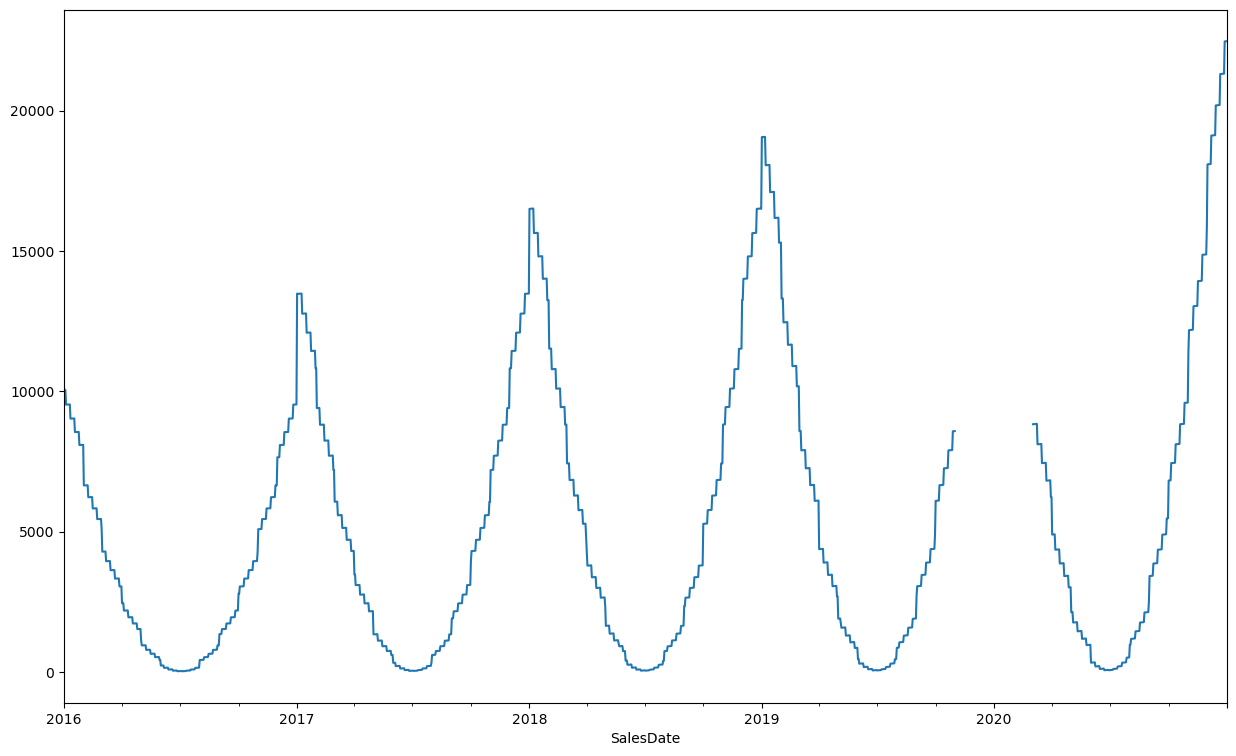
Następnie można uzupełnić dane dokonując predykcji np. w oparciu od dane do połowy roku 2019, jakość predykcji ocenić można przez porównanie z niezaburzonymi obserwacjami, Do predykcji użyjemy tutaj modelu STLForecast, który dekomponuje szereg czasowy na trend, sezonowość i czynnik losowy i wykonuje predykcję odsezonowionych danych z użyciem modelu ARIMA
from statsmodels.tsa.api import STLForecast
from statsmodels.tsa.arima.model import ARIMA
test_start = "2019-07-01"
df_ts.index = pd.DatetimeIndex(df_ts.index.values, freq=df_ts.index.inferred_freq) # ustawienie kroku
df_ts_train = df_ts.loc[df_ts.index<test_start,"SLSU"]
df_ts_test = df_ts.loc[df_ts.index>=test_start, "SLSU"]
model = STLForecast(df_ts_train, ARIMA, model_kwargs={"order": (3,2,3), "enforce_invertibility": False}, period=365)
stl = model.fit()
df_ts.loc[df_ts.index>=test_start, "prediction"] =stl.forecast(len(df_ts_test))
df_ts[["SLSU", "prediction"]].plot(figsize=(15,9))
C:\Users\knajmajer\AppData\Local\anaconda3\envs\jbook\Lib\site-packages\statsmodels\base\model.py:607: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
warnings.warn("Maximum Likelihood optimization failed to "
<Axes: >
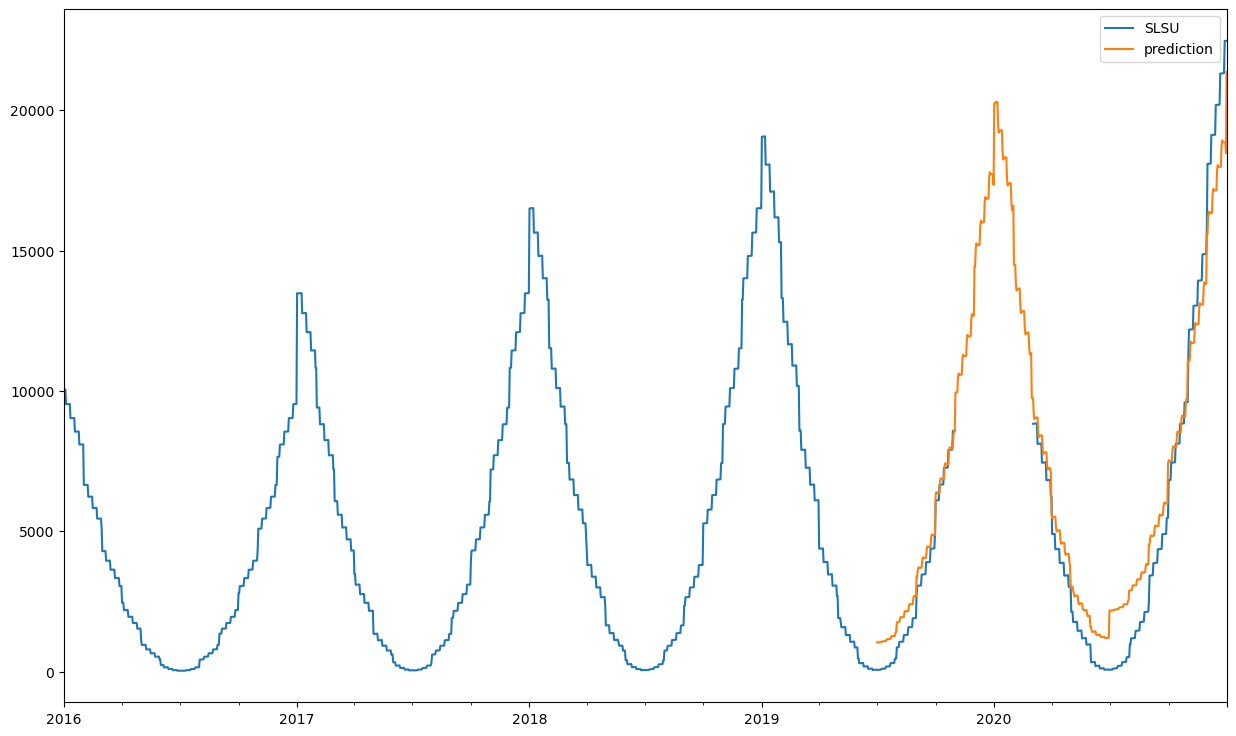
Tym sposobem otrzymujemy oczyszczony szereg czasowy.
df_ts["SLSU"] = df_ts["SLSU"].fillna(df_ts["prediction"])
df_ts["SLSU"].plot(figsize=(15,9))
<Axes: >